题目内容
下列命题中,正确的命题有( )
(1)y=1是幂函数;
(2)用相关指数R2来刻画回归效果,R2越接近0,说明模型的拟合效果越好;
(3)将一组数据中的每个数据都加上或减去一个常数后,方差恒不变;
(4)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=
-p;
(5)回归直线一定过样本中心(
,
).
(1)y=1是幂函数;
(2)用相关指数R2来刻画回归效果,R2越接近0,说明模型的拟合效果越好;
(3)将一组数据中的每个数据都加上或减去一个常数后,方差恒不变;
(4)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=
| 1 |
| 2 |
(5)回归直线一定过样本中心(
. |
| x |
. |
| y |
| A、2个 | B、3个 | C、4个 | D、5个 |
分析:(1)显然错误;(2)相关指数R2用来衡量两个变量之间线性关系的强弱R2越接近于1,说明相关性越强,相反,相关性越小,命题可做判断;(3)利用将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变,故正确.(4)利用正态分布N(0,1)的密度函数的图象,由图象的对称性可得结果.(5)本命题考查回归直线方程,回归直线一定过样本中心(
,
)
. |
| x |
. |
| y |
解答:解:(1)显然错误;
(2)相关指数R2用来衡量两个变量之间线性关系的强弱R2越接近于1,说明相关性越强,相反,相关性越小,因此此命题不正确;
(3)利用将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变,故正确;
(4)由图象的对称性可得,若P(ξ>1)=p,则P(ξ<-1)=p,∴则P(-1<ξ<1)=1-2p,P(-1<ξ<0)=
-p,故正确;
(5)由最小二乘法可知:a=
-b
因此回归直线一定过样本中心(
,
),命题正确;
故选B.
(2)相关指数R2用来衡量两个变量之间线性关系的强弱R2越接近于1,说明相关性越强,相反,相关性越小,因此此命题不正确;
(3)利用将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变,故正确;
(4)由图象的对称性可得,若P(ξ>1)=p,则P(ξ<-1)=p,∴则P(-1<ξ<1)=1-2p,P(-1<ξ<0)=
| 1 |
| 2 |
(5)由最小二乘法可知:a=
. |
| y |
. |
| x |
. |
| x |
. |
| y |
故选B.
点评:本题考查了命题的真假判断,综合考查了相关问题的概念,如:回归直线方程与线性相关性,方差的特点,正态分布的密度函数的图象等

练习册系列答案
相关题目
 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足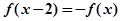 对一切
对一切 恒成立,当
恒成立,当 时,
时, 。则下列四个命
。则下列四个命 是以4为周期的周期函数; ②
是以4为周期的周期函数; ② 上的解析式为
上的解析式为 ;
; ; ④
; ④ 处的切线方程为
处的切线方程为 。
。