题目内容

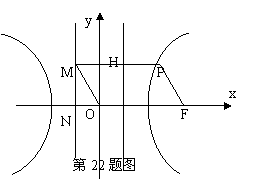
如图，F为双曲线C：＝1(a＞0，b＞0)的右焦点，P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点．已知四边形OFPM为平行四边形，|PF|＝λ|OF|．

(1)写出双曲线C的离心率e与λ的关系式；

(2)当λ＝1时，经过焦点F且平行于OP的直线交双曲线于A、B两点，若|AB|＝12，求此时的双曲线方程．

答案：
解析：

　　解：(1)∵四边形OFPM是平行四边形，

　　∴|OF|＝|PM|＝c，作右准线交PM于H，则|PM|＝|PH|＋2×，

　　又e＝，e2－λe－2＝0．

　　(2)当λ＝1时，e＝2，c＝2a，b2＝3a2，

　　所以双曲线方程为＝1，

　　设P(x0，y0)，则由|OF|＝|PM|，得x0＋＝c；x0＝a；y0＝a．

　　所以直线OP的斜率为，

　　则直线AB的方程为y＝(x－2a)，

　　代入双曲线方程得4x2＋20ax－29a2＝0，

　　又|AB|＝12，

　　由|AB|＝得

　　12＝，

　　解得a2＝1，b2＝3，所以双曲线为x2－＝1．


练习册系列答案
相关题目
精英家教网如图，F为双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点．P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点．已知四边形OFPM为平行四边形，|PF|=λ|OF|．
（Ⅰ）写出双曲线C的离心率e与λ的关系式；
（Ⅱ）当λ=1时，经过焦点F且平行于OP的直线交双曲线于A、B点，若|AB|=12，求此时的双曲线方程．
精英家教网如图，F为双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点．P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点．已知四边形OFPM为平行四边形，|PF|=λ|OF|．
（Ⅰ）写出双曲线C的离心率e与λ的关系式；
（Ⅱ）当λ=1时，设双曲线右支与x轴的交点为R，且|PR|=2，求此时的双曲线方程．
如图，F为双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的右焦点，P为双曲线C右支上一点，且位于x轴上方，M为左准线上一点，O为坐标原点，已知四边形OFPM为平行四形，|
PF
|=λ|
OF
|．写出双曲线C的离心率e与λ的关系式．
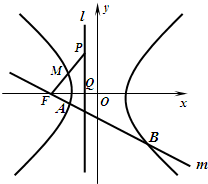如图点F为双曲线C的左焦点，左准线l交x轴于点Q，点P是l上的一点|PQ|=|FQ|=1，且线段PF的中点M在双曲线C的左支上．
（1）求双曲线C的标准方程；
（2）若过点F的直线m与双曲线C的左右两支分别交于A、B两点，设
FB
=λ
FA
，当λ∈[6，+∞）时，求直线m的斜率k的取值范围．

（06年安徽卷）（14分）

如图，F为双曲线C：的右焦点。P为双曲线C右支上一点，且位于轴上方，M为左准线上一点，为坐标原点。已知四边形为平行四边形，。

（Ⅰ）写出双曲线C的离心率与的关系式；

（Ⅱ）当时，经过焦点F且平行于OP的直线交双曲线于A、B点，若，求此时的双曲线方程。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网