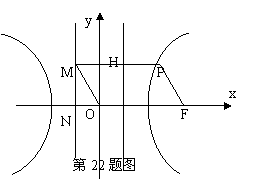
题目内容
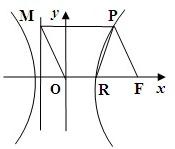 如图,F为双曲线C:
如图,F为双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)写出双曲线C的离心率e与λ的关系式;
(Ⅱ)当λ=1时,设双曲线右支与x轴的交点为R,且|PR|=2,求此时的双曲线方程.
分析:(Ⅰ)根据题意,四边形OFPM是平行四边形,分析可得|OF|=|PM|=c,作双曲线的右准线交PM于H,由双曲线的性质可得|PM|=|PH|+2
,又由e=
,代入化简可得答案;
(Ⅱ)分析可得,当λ=1时,四边形OFPM是菱形,则e=2,即c=2a,可得|OF|=|PF|=2a,可求得点p的横坐标,作PQ⊥x轴,垂足为Q,则点Q为线段RF的中点,进而可得△PQF为等腰三角形,则|PR|=2a=2,即可得a、b的值,由双曲线的标准方程可得答案.
| a2 |
| c |
| |PF| |
| |PH| |
(Ⅱ)分析可得,当λ=1时,四边形OFPM是菱形,则e=2,即c=2a,可得|OF|=|PF|=2a,可求得点p的横坐标,作PQ⊥x轴,垂足为Q,则点Q为线段RF的中点,进而可得△PQF为等腰三角形,则|PR|=2a=2,即可得a、b的值,由双曲线的标准方程可得答案.
解答: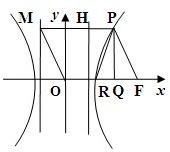 解:(Ⅰ)∵四边形OFPM是平行四边形,
解:(Ⅰ)∵四边形OFPM是平行四边形,
∴|OF|=|PM|=c,
作双曲线的右准线交PM于H,
则|PM|=|PH|+2
,
又e=
=
=
=
=
,
e2-λe-2=0
(Ⅱ)当λ=1时,四边形OFPM是菱形
e=2,c=2a,即|OF|=|PF|=2a,2a=exP-a(或2a=xP+
)
可求得点p的横坐标为eP=
a
作PQ⊥x轴,垂足为Q,则点Q为线段RF的中点,
所以△PQF为等腰三角形,
所以|PR|=2a=2,即a=1,b=
,
双曲线方程为:x2-
=1.
 解:(Ⅰ)∵四边形OFPM是平行四边形,
解:(Ⅰ)∵四边形OFPM是平行四边形,∴|OF|=|PM|=c,
作双曲线的右准线交PM于H,
则|PM|=|PH|+2
| a2 |
| c |
又e=
| |PF| |
| |PH| |
| λ|OF| | ||
c-2
|
| λc | ||
c-2
|
| λc2 |
| c2-2a2 |
| λe2 |
| e2-2 |
e2-λe-2=0
(Ⅱ)当λ=1时,四边形OFPM是菱形
e=2,c=2a,即|OF|=|PF|=2a,2a=exP-a(或2a=xP+
| a2 |
| c |
可求得点p的横坐标为eP=
| 3 |
| 2 |
作PQ⊥x轴,垂足为Q,则点Q为线段RF的中点,
所以△PQF为等腰三角形,
所以|PR|=2a=2,即a=1,b=
| 3 |
双曲线方程为:x2-
| y2 |
| 3 |
点评:本题考查双曲线的几何性质及应用,此类题目一般计算量较大,解本题时,注意把握平行四边形与菱形的性质,寻找突破点,同时可以减小运算量.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
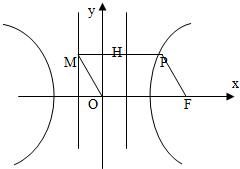 如图,F为双曲线C:
如图,F为双曲线C: 如图,F为双曲线
如图,F为双曲线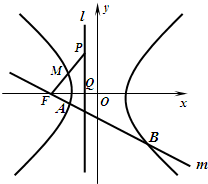 如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.
如图点F为双曲线C的左焦点,左准线l交x轴于点Q,点P是l上的一点|PQ|=|FQ|=1,且线段PF的中点M在双曲线C的左支上.