题目内容
如图, 平面
平面 ,四边形
,四边形 是正方形,
是正方形, ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.

(1)求二面角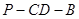 的大小;
的大小;
(2)求证:平面 平面
平面 ;
;
(3)求点 到平面
到平面 的距离。
的距离。
【答案】
略
【解析】解法一:(1)∵ ⊥平面
⊥平面 ,
,
∴  是
是 在平面
在平面 上的射影.
上的射影.
由 是正方形知
是正方形知 ,
,
∴  。
。
∴  是二面角
是二面角 的平面角.
的平面角.
∵  ,∴
,∴  =45º,
=45º,
即二面角 的大小为45º。………3分
的大小为45º。………3分
(2)如图,建立空间直角坐标系至 ,则
,则
 ,
, ,
, ,
,
 ,∵
,∵ 是
是 的中点,∴
的中点,∴  ,
,
∴  ,
, ,
, 。
。
设平面 的一个法向量为
的一个法向量为 ,
,
平面 的一个法向量为
的一个法向量为 。
。
∴  ,
, ,即有
,即有
令 =1,得x1=-2,y1=-1.
=1,得x1=-2,y1=-1.
∴  。
。
同理由 ,
, ,即有
,即有
令z2=1,得x2=0,y2=1,∴  。
。
∵  -2×0+(-1)×1+1×1=0,
-2×0+(-1)×1+1×1=0,
∴  ,[来源:学*科*网Z*X*X*K]
,[来源:学*科*网Z*X*X*K]
∴ 平面MND⊥平面PCD.……………………………………………………………6分
(3)设 到平面
到平面 的距离为
的距离为 由(2)知平面
由(2)知平面 的法向量
的法向量
∵  ,
,
∴ | |=4,又 |
|=4,又 | |=
|= ,
,
∴  =
=
即点P到平面MND的距离为 .………………………………………………10分
.………………………………………………10分
解法二:(1)同解法一.
(2)作 的中点
的中点 ,连接
,连接 ,如图.
,如图.
∵  平行且等于
平行且等于 ,
, 平行且等于
平行且等于 ,
,
∴  与
与 平行且相等,于是四边形
平行且相等,于是四边形 是平行四边形,∴
是平行四边形,∴  //
// 。
。
∵  ,∴
,∴  。∵
。∵  面
面 ,∴
,∴  。又∵
。又∵  ,
,
∴  ⊥面
⊥面 。∴
。∴  。∴
。∴  ⊥面
⊥面 。∴
。∴  ⊥面
⊥面 。
。
 又∵
又∵ 面
面 ,∴ 平面
,∴ 平面 ⊥平面
⊥平面 。……………………6分
。……………………6分
(3)设 到平面
到平面 的距离为
的距离为 ,
,
由 ,有
,有 ,
,
即 ,
,
∴  。
。
∵ 在 中,
中, .
.
又 ,
, ,∴
,∴ ,
,
即 到平面
到平面 的距离为
的距离为 。…………………………………………………10分
。…………………………………………………10分

练习册系列答案
相关题目

 平面
平面 ,四边形
,四边形 ,点
,点 、
、 、
、 分别为线段
分别为线段 、
、 和
和 的中点. 在线段
的中点. 在线段 ,使得点
,使得点 到平面
到平面 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段 的长;
的长;
 平面
平面 ,四边形
,四边形 ,点
,点 、
、 、
、 分别为线段
分别为线段 、
、 和
和 的中点.
的中点. 与
与 所成角的余弦值;
所成角的余弦值; ,使得点
,使得点 到平面
到平面 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.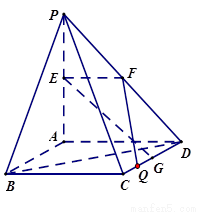
 平面
平面 ,四边形
,四边形 ,
, 与平面
与平面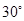 ,点
,点 是
是 的中点,点
的中点,点 在矩形
在矩形 上移动.
上移动. ;
; 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.