题目内容
非零向量 与
与 满足
满足 且
且 ,则⊿ABC为( )
,则⊿ABC为( )
| A.三边均不等的三角形 | B.直角三角形 |
| C.等边三角形 | D.等腰非等边三角形 |
C
解析试题分析:由 ,则
,则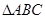 的角
的角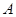 的平分线与
的平分线与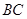 垂直,因为
垂直,因为 ,
,
所以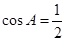 ,即
,即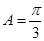 ,所以
,所以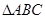 是等边三角形.
是等边三角形.
考点:平面向量的数量积,等边三角形的性质.

练习册系列答案
相关题目
在 中,
中, 是
是 的中点,
的中点,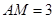 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于
等于
A. | B. | C. | D. |
设 是非零向量,已知命题P:若
是非零向量,已知命题P:若 ,
, ,则
,则 ;命题q:若
;命题q:若 ,则
,则 ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A.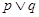 | B.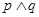 | C. | D. |
设点 为椭圆
为椭圆 上两点.点
上两点.点 关于
关于 轴对称点为
轴对称点为 (异于点
(异于点 ).若直线
).若直线 分别与
分别与 轴交于点
轴交于点 , 则
, 则 =( )
=( )
| A.0 | B.1 | C. | D.2 |
 ,向量
,向量 与
与 的位置关系为( )
的位置关系为( )
| A.平行 | B.垂直 | C.不平行也不垂直 | D.夹角为 |
在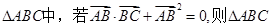 是( )
是( )
| A.锐角三角形 | B.钝角三角形 |
| C.直角三角形 | D.等腰直角三角形 |
已知平面向量a,b,|a|=1,|b|=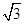 ,且|2a+b|=
,且|2a+b|=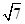 ,则向量a与向量a+b的夹角为( )
,则向量a与向量a+b的夹角为( )
A.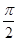 | B. | C.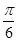 | D.π |
已知向量a=(1,k),b=(2,2),且a+b与a共线,那么a·b的值为( )
| A.1 | B.2 | C.3 | D.4 |
 ),
), .
. )
) 若
若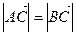 ,求角
,求角 的值; (2)若
的值; (2)若 ,求
,求 .
.