题目内容
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直。若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(1)求证:平面ABD⊥平面ACD;
(2)求二面角A―CD―B的平面角的正切值;
(3)设过直线AD且与BC平行的平面为![]() ,求点B到平面
,求点B到平面![]() 的距离。
的距离。
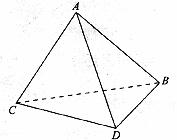
解:(1)平面BCD⊥平面ABC,BD⊥BC,平面BCD![]() 平面ABE=BC,∴BD⊥平面ABC,
平面ABE=BC,∴BD⊥平面ABC,
∵![]() ∴
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() 。
。
(2)设BC中点为E,连接AE,过E作EF⊥CD于F,连接AF。
由三垂线定理得![]() 为二面角的平面角。
为二面角的平面角。
由![]() ∽
∽![]() 可求得
可求得![]() ,又AE=3,
,又AE=3,
所以![]() ,即二面角的平面角的正切值为2。
,即二面角的平面角的正切值为2。
(3)过点D作DG∥BC,且CB=DG,连接AG。
则平面ADG为平面![]()
∵BC∥平面ADG,
所以B到平面ADG的距离与C到平面ADG的距离相等,设为![]() ,
,
∵![]() ,∴
,∴![]() 。
。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
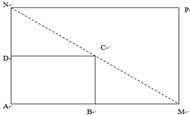 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上D点在AN上,且对角线MN过点C,已知AB=3米,AD=2米.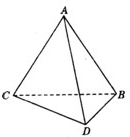 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.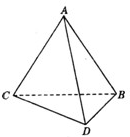 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.