Question

【题目】在一次篮球定点投篮训练中，规定每人最多投3次，在处每投进一球得3分；在处每投进一球得2分．如果前两次得分之和超过3分就停止投篮；否则投第三次．某同学在处的投中率，在处的投中率为，该同学选择先在处投第一球，以后都在处投，且每次投篮都互不影响，用表示该同学投篮训练结束后所得的总分，其分布列为：

	0	2	3	4	5
	0.03

（1）求的值；

（2）求随机变量的数学期望；

（3）试比较该同学选择上述方式投篮得分超过3分与选择都在处投篮得分超过3分的概率的大小．

Answer 1

【答案】（1）（2）（3） 该同学选择都在处投篮得分超过分的概率大

【解析】试题分析：（1）根据，解得；（2）根据相互独立事件概率计算公式，计算得，由此计算得期望为；（3）用表示事件“该同学在处投第一球，以后都在处投，得分超过分”，用表示事件“该同学都在处投，得分超过分”，计算得, .

试题解析：

（1）由题意可知， 对应的事件为“三次投篮没有一次投中”，

∴，

∵，解得；

（2）根据题意， ，

， ，

∴，

（3）用表示事件“该同学在处投第一球，以后都在处投，得分超过3分”，用表示事件“该同学都在处投，得分超过3分”，

，∴，

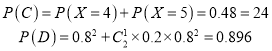即该同学选择都在处投篮得分超过3分的概率的大于该同学在处投第一球，以后都在处投，得分超过3分的概率．