题目内容
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名, 以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎, 小数点后的一位数字为叶)：
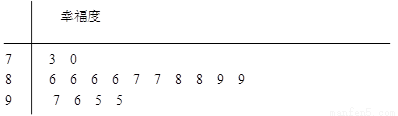
(1) 指出这组数据的众数和中位数；
(2) 若幸福度不低于9.5分, 则称该人的幸福度为“极幸福”.求从这16人中随机选取3人, 至多有1人是“极幸福”的概率；
(3) 以这16人的样本数据来估计整个社区的总体数据, 若从该社区(人数很多)任选3人, 记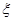
表示抽到“极幸福”的人数, 求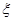的分布列及数学期望．
【答案】
(1) 众数：8.6；中位数：8.75 (2)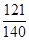
(3)分布列为
|
|
|
|
|
|
|
|
|
|
|
|
.
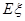
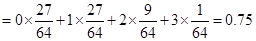【解析】
试题分析：(1)众数：8.6；中位数：8.75 2分
(2)设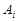
表示所取3人中有
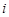个人是“极幸福”, 至多有1人是“极幸福”记为事件
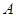, 则
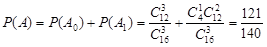6分
(3)
的可能取值为0、1、2、3 7分
； 
； 
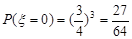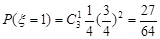
分布列为
|
|
|
|
|
|
|
|
|
|
|
|
11分
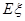
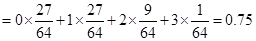. 12分
另解：的可能取值为0、1、2、3 7分
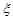∽B（3, 
）, 
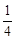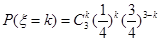. 9分
分布列为
|
|
|
|
|
|
|
|
|
|
|
|
10分
所以=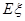
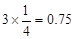. 12分
考点：茎叶图，古典概型概率及分布列
点评：众数是出现次数最多的数，中位数是由小到大排列后位于中间的数，古典概型概率首先找到所有基本事件种数及满足题意要求的基本事件种数，然后求其比值；分布列的求解步骤：找到随机变量可取的值，求出各值的概率，列表写成分布列
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
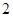
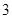
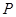
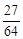
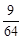
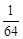
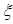
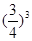
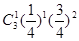
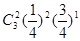
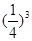
（2013•广州三模）某网站用“10分制”调查一社区人们的幸福度．现从调查人群中随机抽取16名，以下茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：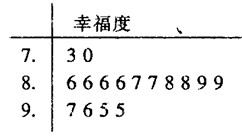
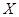表示抽到“极幸福”的人数，求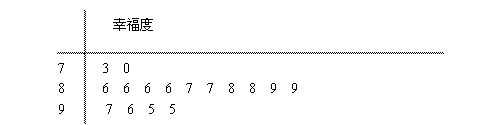
表示抽到“极幸福”的人数，求
某网站用“10分制”调查一社区人们的幸福度．现从调查人群中随机抽取16名，以下茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：