题目内容
7.(理)已知圆心为O,半径为1的圆上有不同的三个点A、B、C,其中$\overrightarrow{OA}•\overrightarrow{OB}=0$,存在实数λ,μ满足$\overrightarrow{OC}+λ\overrightarrow{OA}+u\overrightarrow{OB}=\overrightarrow 0$,则实数λ,μ的关系为( )| A. | λ2+μ2=1 | B. | $\frac{1}{λ}+\frac{1}{μ}=1$ | C. | λμ=1 | D. | λ+μ=1 |
分析 由题意可得|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1,且$\overrightarrow{OA}•\overrightarrow{OB}=0$,再把 $\overrightarrow{OC}$=-λ$\overrightarrow{OA}$-μ$\overrightarrow{OB}$,平方可得结论.
解答 解:由题意可得|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1,且$\overrightarrow{OA}•\overrightarrow{OB}=0$.
∵$\overrightarrow{OC}+λ\overrightarrow{OA}+u\overrightarrow{OB}=\overrightarrow 0$,即 $\overrightarrow{OC}$=-λ$\overrightarrow{OA}$-μ$\overrightarrow{OB}$,平方可得 1=λ2+μ2,
故选:A.
点评 本题主要考查圆的定义及向量的模及其数量积运算,还考查了向量与实数的转化.在向量的加,减,数乘和数量积运算中,数量积的结果是实数,所以考查应用较多,属于基础题.

练习册系列答案
相关题目
15.如图,ABCDEF是正六边形,下列等式成立的是( )


| A. | $\overrightarrow{AE}$•$\overrightarrow{FC}$=0 | B. | $\overrightarrow{AE}$•$\overrightarrow{DF}$>0 | C. | $\overrightarrow{FC}$=$\overrightarrow{FD}$+$\overrightarrow{FB}$ | D. | $\overrightarrow{FD}$•$\overrightarrow{FB}$<0 |
19. 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
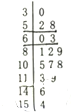
甲市2015年2月份中有15对空气质量指数PM2.5进行监测,获得PM2.5日均浓度数据茎叶图如图所示.
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.
 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
(Ⅰ)在15天内任取2天,求甲市空气质量类别均为良的概率;
(Ⅱ)在15天内任取2天,记甲市空气质量级别不超过三级的天数为X,求随机变量X的分布列及数学期望.
16.若一个底面是正三角形的三棱柱的主视图如图所示,则其侧面积为( )


| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 6 |
 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格. 在如图所示的几何体中,四边形CDPQ为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面CDPQ⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.
在如图所示的几何体中,四边形CDPQ为矩形,四边形ABCD为直角梯形,且∠BAD=∠ADC=90°,平面CDPQ⊥平面ABCD,AB=AD=$\frac{1}{2}$CD=1,PD=$\sqrt{2}$.