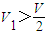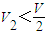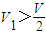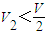Question

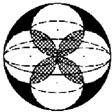
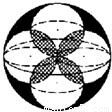
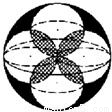
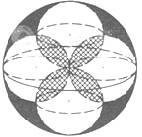
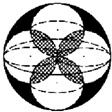如图，体积为V的大球内有4个小球，每个小球的球面过大球球心且与大球球面有且只有一个交点，4个小球的球心是以大球球心为中心的正方形的4个顶点．V₁为小球相交部分（图中阴影部分）的体积，V₂为大球内、小球外的图中黑色部分的体积，则下列关系中正确的是（　　）

• A、V1＞

  V

  2

• B、V2＜

  V

  2

• C、V₁＞V₂
• D、V₁＜V₂

Answer 1

分析：根据题意推知小球半径是大球的一半，建立大球体积小球体积和阴影部分的体积的关系，可推知选项．

解答：解：设大球的半径为R，则小球的半径为：

R

2

，
由题意可得：V=

4π

3

R3=4•

4π

3

(

R

2

)3-V1+V2
所以  V2-V1=

4π

3

R3-4•

4π

3

(

R

2

)3=

2π

3

R3 =

V

2

＞0
即：V₂＞V₁
故选D．

点评：本题考查组合体的体积，空间想象能力，逻辑推理能力，是难题．