题目内容
对于在区间 上有意义的两个函数
上有意义的两个函数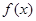 和
和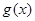 ,如果对于任意的
,如果对于任意的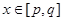 ,都有
,都有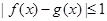 ,则称
,则称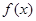 与
与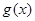 在区间
在区间 上是接近的两个函数,否则称它们在
上是接近的两个函数,否则称它们在 上是非接近的两个函数。现有两个函数
上是非接近的两个函数。现有两个函数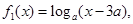 ,
,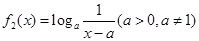 ,且
,且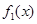 与
与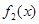 在
在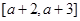 都有意义.
都有意义.
(1)求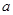 的取值范围;
的取值范围;
(2)讨论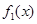 与
与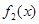 在区间
在区间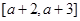 上是否是接近的两个函数.
上是否是接近的两个函数.
【答案】
(1) (2)当
(2)当 时,
时, 与
与 是接近的;当
是接近的;当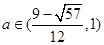 时,
时, 与
与 是非接近的
是非接近的
【解析】
试题分析:(1)显然 且
且 ,则
,则 ,
,
而 、
、 在
在 上有意义,当且仅当
上有意义,当且仅当 ,从而
,从而
(2)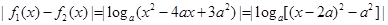
当 时,
时,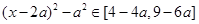
则 ,
,
则
 欲使
欲使 ,必有
,必有
解得
即当 时,
时, 与
与 是接近的;当
是接近的;当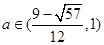 时,
时, 与
与 是非接近的.
是非接近的.
考点:函数定义域,最值及新信息的读取理解能力
点评:求解本题第二问先要读懂给定信息的含义,即 的范围要在
的范围要在 之间,进而找到思路:需求
之间,进而找到思路:需求 的值域,转化为对数函数二次函数求值域
的值域,转化为对数函数二次函数求值域

练习册系列答案
相关题目
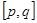 上有意义的两个函数
上有意义的两个函数 ,如果对于任意的
,如果对于任意的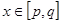 ,都有
,都有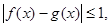 则称
则称 给定一个区间
给定一个区间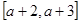 。
。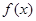 在区间
在区间 的取值范围;
的取值范围; 在区间
在区间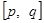 上有意义的两个函数
上有意义的两个函数 和
和 ,如果对于任意的
,如果对于任意的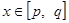 ,都有
,都有 ,则称
,则称 ,给定一个区间
,给定一个区间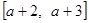 。
。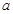 的取值范围;
的取值范围; 上有意义的两个函数
上有意义的两个函数 ,如果对任意
,如果对任意 均有
均有 ,则称
,则称 ,给定区间
,给定区间 .
. 在给定区间
在给定区间 的取值范围;
的取值范围;