题目内容
四面体的六条棱中,有五条棱长都等于a,则该四面体的体积的最大值为( )
A.
| B.
| C.
| D.
|
若一个四面体有五条棱长都等于a,
则它必然有两个面为等边三角形,如下图
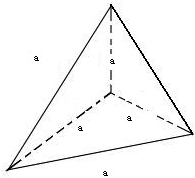
由图结合棱锥的体积公式,
当这两个平面垂直时,底面积是定值,高最大,
故该四面体的体积最大,
此时棱锥的底面积S=
×a2×sin60°=
a2,
棱锥的高h=
a,
则该四面体的体积最大值为V=
×
a2×
a=
a3.
故选C.
则它必然有两个面为等边三角形,如下图

由图结合棱锥的体积公式,
当这两个平面垂直时,底面积是定值,高最大,
故该四面体的体积最大,
此时棱锥的底面积S=
| 1 |
| 2 |
| ||
| 4 |
棱锥的高h=
| ||
| 2 |
则该四面体的体积最大值为V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 8 |
故选C.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目