题目内容
已知二次函数y=ax2+bx+c在（-1，+∞）上为减函数，则f（0）＞0，则直线ax+by+c=0不经过第分析：先根据条件判断直线方程中未知数系数的符号及常数项的符号，进而判断直线的斜率的符号、在纵轴上的截距的符号，
从而确定直线在坐标系中的位置．
从而确定直线在坐标系中的位置．
解答：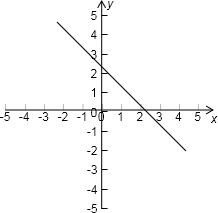
解：∵二次函数y=ax2+bx+c在（-1，+∞）上为减函数，
∴对称轴-
≤-1，且a＜0，
∴b＜0，
∵f（0）＞0，∴c＞0，
∴直线ax+by+c=0 的斜率-
＜0，在纵轴上的截距-
＞0，
故直线不经过第三象限，
故答案为三．
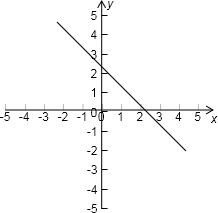解：∵二次函数y=ax2+bx+c在（-1，+∞）上为减函数，∴对称轴-
| b |
| 2a |
∴b＜0，
∵f（0）＞0，∴c＞0，
∴直线ax+by+c=0 的斜率-
| a |
| b |
| c |
| b |
故直线不经过第三象限，
故答案为三．
点评：本题考查确定直线位置的几何要素，二次函数的单调区间、单调性的应用，体现数形结合的数学思想．
练习册系列答案
相关题目