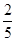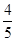题目内容
甲盒中有一个红色球,两个白色球,这3个球除颜色外完全相同,有放回地连续抽取2个,每次从中任意地取出1个球,用列表的方法列出所有可能结果,计算下列事件的概率
(Ⅰ)取出的2个球都是白球,(Ⅱ)取出的两个球至少有一个是白球.
(Ⅰ)取出的2个球都是白球,(Ⅱ)取出的两个球至少有一个是白球.
 (Ⅱ)
(Ⅱ)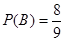
本题两问都属于古典概型,要先求出所有试验的结果,然后分别求出事件包含的结果数,用事件包含的结果数除以试验的结果数,即可得出事件发生的概率.
记红色球为1,两个白色球分别为2,3
那么有放回地连续取2个球,每次从中任意取出1个球,共有9种不同的结果:(1,1),(1,2),(1,3)(2,1),(2,2),(2,3)(3,1),(3,2),(3,3)
(Ⅰ)记事件A:取出的2个球都是白球事件A包含6种不同的结果 ∴
(Ⅱ)记事件B:取出的2个球至少有一个是白球 事件B包含8种不同结果 ∴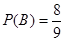
记红色球为1,两个白色球分别为2,3
那么有放回地连续取2个球,每次从中任意取出1个球,共有9种不同的结果:(1,1),(1,2),(1,3)(2,1),(2,2),(2,3)(3,1),(3,2),(3,3)
(Ⅰ)记事件A:取出的2个球都是白球事件A包含6种不同的结果 ∴

(Ⅱ)记事件B:取出的2个球至少有一个是白球 事件B包含8种不同结果 ∴

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
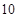 件产品中,有
件产品中,有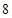 件合格品,
件合格品,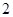 件次品.从这
件次品.从这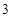 件,抽出的
件,抽出的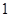 件次品的概率为
件次品的概率为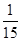

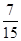
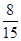
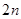 位数
位数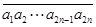 (其中
(其中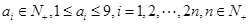 )满足:
)满足: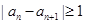 ,
,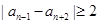 ,
, ,
,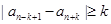 ,
,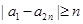 (其中
(其中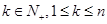 ),则称
),则称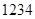 就是一个“4位参差数”.由
就是一个“4位参差数”.由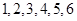 组成无重复数字的
组成无重复数字的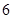 位数,则组成的
位数,则组成的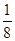
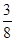
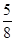
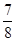
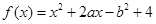 .
.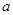 是从-2、-1、0、1、2五个数中任取的一个数,
是从-2、-1、0、1、2五个数中任取的一个数,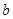 是从0、1、2三个数中任取的一个数,求函数
是从0、1、2三个数中任取的一个数,求函数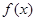 无零点的概率;
无零点的概率;
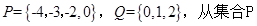 中随机取一个数作为
中随机取一个数作为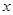 ,从集合
,从集合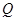 中随机取一个数
中随机取一个数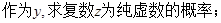
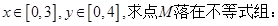
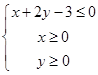 所表示的平面区域内的概率。
所表示的平面区域内的概率。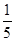
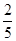
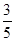
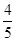
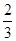
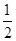
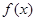 ,
, 都是定义在R上的函数,
都是定义在R上的函数, ,且
,且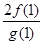

 =
= .现任取正整数
.现任取正整数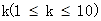 ,则在有穷数列{
,则在有穷数列{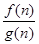 }(n=1,2,¼,10)中前k项和大于
}(n=1,2,¼,10)中前k项和大于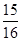 的概率是( )
的概率是( )