题目内容
已知△ABC的面积为S，角A、B、C的对边分别为a、b、c，若4S=a2+b2-c2，那么C= ．
【答案】分析：利用余弦定理及三角形的面积公式对已知条件进行化简可得，sinC=cosC，结合三角形的内角范围可求角C
解答：解：∵4s=a2+b2-c2
∴
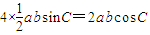
化简可得，sinC=cosC
∵0＜C＜π
∴
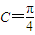
故答案为：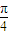
点评：本题主要考查了三角形的面积公式及余弦定理的应用，属于基础试题．
解答：解：∵4s=a2+b2-c2
∴
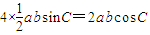
化简可得，sinC=cosC
∵0＜C＜π
∴
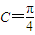
故答案为：
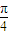
点评：本题主要考查了三角形的面积公式及余弦定理的应用，属于基础试题．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使
（2012•温州一模）如图，在△ABC中，AD⊥BC，垂足为D，且BD：DC：AD=2：3：6．