题目内容
已知不等式(x-1)2≤a2,(a>0)的解集为A,函数f(x)=lg| x-2 |
| x+2 |
(Ⅰ)若A∩B=φ,求a的取值范围;
(Ⅱ)证明函数f(x)=lg
| x-2 |
| x+2 |
分析:(I)有不等式(x-1)2≤a2,(a>0)解出集合A,再有函数f(x)=lg
的定义域为B,求出集合B,利用A∩B=φ,求a的取值范围;
(II)先有f(x)的解析式求得该函数的定义域,再利用奇函数的图象关于原点对称进而把问题转化为判断函数的奇偶性.
| x-2 |
| x+2 |
(II)先有f(x)的解析式求得该函数的定义域,再利用奇函数的图象关于原点对称进而把问题转化为判断函数的奇偶性.
解答:解:(Ⅰ)由(x-1)2≤a2,(a>0),得1-a≤x≤1+a,A=x|1-a≤x≤1+a,
由
>0得x<-2或x>2,B=x|x<-2或x>2,
∵A∩B=φ,∴-2≤1-a且1+a≤2(a>0),∴0<a≤1;
(Ⅱ)证明:∵f(x)=lg
(x<-2或x>2),
∴f(x)+f(-x)=lg
+lg
=lg(
×
)=lg1=0
∴f(-x)=-f(x),∴f(x)为奇函数,
∴f(x)的图象关于原点对称.
由
| x-2 |
| x+2 |
∵A∩B=φ,∴-2≤1-a且1+a≤2(a>0),∴0<a≤1;
(Ⅱ)证明:∵f(x)=lg
| x-2 |
| x+2 |
∴f(x)+f(-x)=lg
| x-2 |
| x+2 |
| -x-2 |
| -x+2 |
| x-2 |
| x+2 |
| x+2 |
| x-2 |
∴f(-x)=-f(x),∴f(x)为奇函数,
∴f(x)的图象关于原点对称.
点评:此题考查了一元二次不等式的求解,还考查了学生的等价转化的能力及奇函数的定义与判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
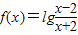 的定义域为B.
的定义域为B.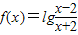 的图象关于原点对称.
的图象关于原点对称.