题目内容
(08年泉州一中适应性练习理)(12分)
在三棱锥P-ABC中,PA⊥底面ABC,PA=AB=BC=2,∠ABC=90°,M为棱PC的中点.
(1)求证:点P,A,B,C四点在同一球面上;
(2)求二面角A-MB-C的大小;
(3)求过P、A、B、C四点的球面中,A、B两点的球面距离.
(1)证明:由已知条件Rt![]() 中PM=MC,则MP=MC=MA,
中PM=MC,则MP=MC=MA,
∵PA⊥平面ABC,AB是PB在平面ABC上的射影,∴PB⊥BC,AB⊥BC
则MC=MB=MP,所以MP=MC=MA=MB,即P,A,B,C四点都在以M为球心,半径为PM的球面上,
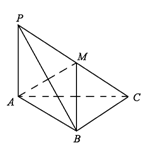
(2)以AC为y轴,AP为z轴建立如图所示的空间直角坐标系A-xyz,
则![]() ,
,![]() ,
,![]()
设平面AMB的法向量为![]() ,∵
,∵![]() ,
,![]() ,
,
由![]() 得
得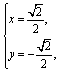 所以
所以![]()
同理设平面BMC的法向量为![]() ,则
,则![]() 解得
解得![]()
所以![]() . 故二面角
. 故二面角![]() 的大小为120°.
的大小为120°.
(3)∵过P,A,B,C四点的球面的球心为M,半径为![]() ,AB=2,
,AB=2,
在![]() 中,
中,![]() ,∴
,∴![]()
故A,B两点的球面距离为![]()

练习册系列答案
相关题目
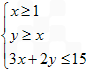 ,则w=log3(2x+y)的最大值是( )。
,则w=log3(2x+y)的最大值是( )。