题目内容
 且
且 ,则
,则 的最小值为
的最小值为

解析试题分析:因为 ,那么
,那么 ,可知
,可知 ,那么所求的表达式为
,那么所求的表达式为 ,结合二次函数的开口方向向上,对称轴为y=
,结合二次函数的开口方向向上,对称轴为y= ,而定义域为
,而定义域为 ,可知函数的最小值为当y=
,可知函数的最小值为当y= 时取得,且为
时取得,且为 ,故答案为
,故答案为 。
。
考点:本试题考查了不等式的最值运用。
点评:解决该试题的关键是对于消元 思想运用,以及结合二次函数的性质求解最值的熟练性,那么同时要注意变元的取值范围这是个易错点,要注意说明范围,考查了分析我难题和解决问题的能力,属于中档题,

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
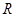 上的函数
上的函数 满足以下条件:
满足以下条件: (2)对任意
(2)对任意 .
. ;②
;② ;③
;③ ;④
;④ .其中一定成立的是 (请写出所有正确的序号)
.其中一定成立的是 (请写出所有正确的序号)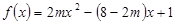 ,
, ,对
,对 R,
R, 与
与 的值至少有一个为正数,则
的值至少有一个为正数,则 的取值范围是 .
的取值范围是 . 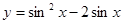 的值域是
的值域是 ;
; ,如果
,如果 ,则
,则 的取值范围是 .
的取值范围是 . ,定义运算“
,定义运算“ ”、“
”、“ ”为:
”为:
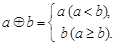
 ,②
,② ,
, , ④
, ④ .
. 在(0,+∞)上为增函数,且
在(0,+∞)上为增函数,且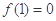 ,则不等式
,则不等式 的解集是 .
的解集是 . 的定义域为 .
的定义域为 .