题目内容
已知椭圆中心在坐标原点O,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),直线l平行OM,且与椭圆交于A、B两个不同的点.(1)求椭圆方程;
(2)若∠AOB为钝角,求直线l在y轴上的截距m的取值范围;
(3)求证直线MA、MB与x轴围成的三角形总是等腰三角形.
【答案】分析:(1)设椭圆方程 ,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;
,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;
(2)设l方程与椭圆方程联立,利用韦达定理及∠AOB为钝角,结合向量知识,即可求直线l在y轴上的截距m的取值范围;
(3)依题即证kAM+kBM=0,利用韦达定理代入,即可证得结论.
解答:(1)解:设椭圆方程 ,依题意可得
,依题意可得 …2分
…2分
可得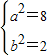 ,所以椭圆方程为
,所以椭圆方程为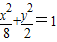 ….4分
….4分
(2)解:设l方程为: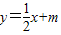 ,与椭圆方程联立得:x2+2mx+2m2-4=0
,与椭圆方程联立得:x2+2mx+2m2-4=0
由韦达定理得:x1+x2=-2m,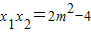 …6分
…6分
设A(x1,y1),B(x2,y2),
因为∠AOB为钝角,所以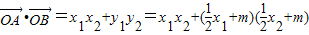
=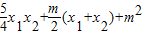 =
= …7分
…7分
又直线l平行OM,∴ ….8分
….8分
(3)证明:依题即证kAM+kBM=0…9分
而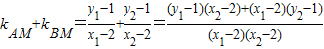 ..…10分
..…10分
将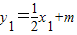 ,
, 代入上式,得
代入上式,得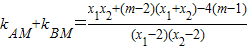 ….12分
….12分
将(2)中韦达定理代入得,上式=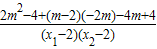 =0
=0
即证.…14分
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
 ,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;
,利用长轴长是短轴长的2倍,且经过点M(2,1),建立方程组,即可求得椭圆方程;(2)设l方程与椭圆方程联立,利用韦达定理及∠AOB为钝角,结合向量知识,即可求直线l在y轴上的截距m的取值范围;
(3)依题即证kAM+kBM=0,利用韦达定理代入,即可证得结论.
解答:(1)解:设椭圆方程
 ,依题意可得
,依题意可得 …2分
…2分可得
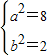 ,所以椭圆方程为
,所以椭圆方程为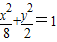 ….4分
….4分(2)解:设l方程为:
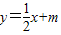 ,与椭圆方程联立得:x2+2mx+2m2-4=0
,与椭圆方程联立得:x2+2mx+2m2-4=0由韦达定理得:x1+x2=-2m,
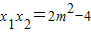 …6分
…6分设A(x1,y1),B(x2,y2),
因为∠AOB为钝角,所以
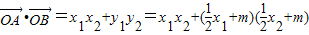
=
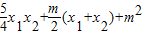 =
= …7分
…7分又直线l平行OM,∴
 ….8分
….8分(3)证明:依题即证kAM+kBM=0…9分
而
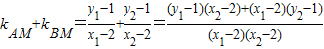 ..…10分
..…10分将
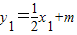 ,
, 代入上式,得
代入上式,得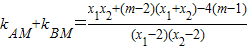 ….12分
….12分将(2)中韦达定理代入得,上式=
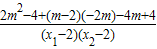 =0
=0即证.…14分
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目