题目内容
双曲线的中心在坐标原点，离心率等于2，一个焦点的坐标为（0，2），则此双曲线的方程是分析：有已知条件列出方程求出a，利用双曲线的三参数的关系，求出b，据双曲线焦点的位置写出双曲线的方程．
解答：解：∵离心率等于2，一个焦点的坐标为（0，2），
∴
=2， c=2且焦点在x轴上，
∴a=1
∵c2=a2+b2
∴b2=3．
所以双曲线的方程为y2-
=1．
故答案为y2-
=1
∴
| c |
| a |
∴a=1
∵c2=a2+b2
∴b2=3．
所以双曲线的方程为y2-
| x2 |
| 3 |
故答案为y2-
| x2 |
| 3 |
点评：求圆锥曲线的方程关键先判断出焦点的位置、考查双曲线中三参数的关系为c2=a2+b2，注意与椭圆中三个参数关系的区别．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，双曲线的中心在坐标原点，焦点在x轴上，F1，F2分别为左、右焦点，双曲线的左支上有一点P，∠F1PF2=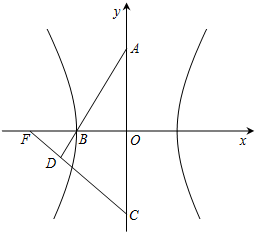
如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（ ）
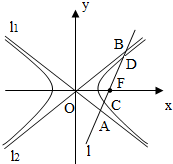如图，双曲线的中心在坐标原点O，焦点在x轴上，两条渐近线分别为l1，l2，经过右焦点F垂直于l1的直线分别交l1，l2于A，B两点．又已知该双曲线的离心率