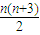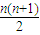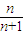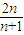题目内容
令an为(1+x)n+1的展开式中含xn-1项的系数,则数列{
}的前n项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:利用二项展开式的通项公式求出通项,令x的指数等于n-1,求出an;利用裂项求和求出数列的前n项和.
解答:解:∵Tr+1=Cn+1rxr,
∴an=Cn+1n-1=Cn-12=
,
=
=2(
-
),
∴
=2(1-
+
-
++
-
)=
.
故选D
∴an=Cn+1n-1=Cn-12=
| n(n+1) |
| 2 |
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| n |
 |
| t-1 |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2n |
| n+1 |
故选D
点评:本题考查二项展开式的通项公式;本题考查利用裂项求数列的前n项和.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
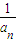 }的前n项和为( )
}的前n项和为( )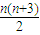
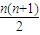
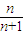
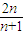
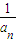 }的前n项和为( )
}的前n项和为( )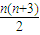
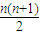
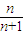
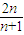
 }的前n项和为( )
}的前n项和为( )



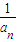 }的前n项和为( )
}的前n项和为( )