题目内容
在两个各项均为正数的数列an、bn(n∈N*)中,已知an、bn2、an+1成等差数列,并且bn2、an+1、bn+12成等比数列.(Ⅰ)证明:数列bn是等差数列;
(Ⅱ)若a1=2,a2=6,设
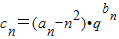 (q>0为常数),求数列cn的前n项和Sn
(q>0为常数),求数列cn的前n项和Sn
【答案】分析:(Ⅰ)根据等差数列和等比数列的性质联立方程求得an+1=bnbn+1,进而求得an=bn-1bn,代入2bn2=an+an+1,求得2bn=bn-1+bn+1,判断出数列bn是等差数列.
(Ⅱ)2bn2=an+an+1求得b1,根据(1)中的结论求得数列{bn}的通项公式,进而根据an=bn-1bn,求得an.进而Cn的通项公式可得先看当q=1时,Cn=n,进而根据等差数列的求和公式求得前n项的和;再看q≠0时,应用错位相减法求得前n项的和.最后综合可得答案.
解答:解:(I)由题意知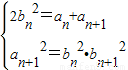 ,
,
又∵数列an、bn各项都是正数,∴an+1=bnbn+1,则an=bn-1bn
代入2bn2=an+an+1,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1,所以数列bn是等差数列.
(II)∵a1=2,a2=6,又2bn2=an+an+1,得2b12=a1+a2=8,解得b1=2
又∵a2=b1b2=6∴b2=3,由(I)知数列bn是等差数列,则公差d=b2-b1=1
∴bn=b1+(n-1)d=2+n-1=n+1,
又an=bn-1bn,得an=n(n+1)=n2+n,
∴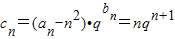 ,
,
则当q=1时,cn=n,此时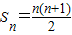 ;
;
当q≠1时,Sn=c1+c2++cn=1×q2+2×q3++nqn+1,①
所以qSn=qc1+qc2++qcn=1×q3+2×q4++nqn+2②
由①-②,得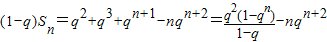 ,
,
即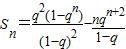
综上可知,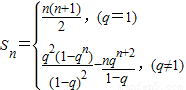
点评:本题主要考查了数列的求和问题.考查了学生对等比数列和等差数列基础知识的掌握.
(Ⅱ)2bn2=an+an+1求得b1,根据(1)中的结论求得数列{bn}的通项公式,进而根据an=bn-1bn,求得an.进而Cn的通项公式可得先看当q=1时,Cn=n,进而根据等差数列的求和公式求得前n项的和;再看q≠0时,应用错位相减法求得前n项的和.最后综合可得答案.
解答:解:(I)由题意知
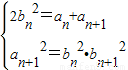 ,
,又∵数列an、bn各项都是正数,∴an+1=bnbn+1,则an=bn-1bn
代入2bn2=an+an+1,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1,所以数列bn是等差数列.
(II)∵a1=2,a2=6,又2bn2=an+an+1,得2b12=a1+a2=8,解得b1=2
又∵a2=b1b2=6∴b2=3,由(I)知数列bn是等差数列,则公差d=b2-b1=1
∴bn=b1+(n-1)d=2+n-1=n+1,
又an=bn-1bn,得an=n(n+1)=n2+n,
∴
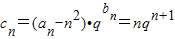 ,
,则当q=1时,cn=n,此时
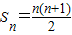 ;
;当q≠1时,Sn=c1+c2++cn=1×q2+2×q3++nqn+1,①
所以qSn=qc1+qc2++qcn=1×q3+2×q4++nqn+2②
由①-②,得
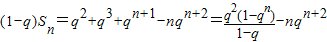 ,
,即
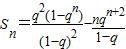
综上可知,
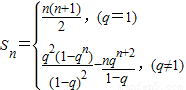
点评:本题主要考查了数列的求和问题.考查了学生对等比数列和等差数列基础知识的掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在各项均为正数的等比数列{ }中,
}中,  、
、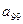 是方程
是方程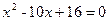 的两个根,则
的两个根,则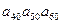 的值为
的值为
| A.32 | B.64 | C. 64 64 | D.256 |