题目内容
在两个各项均为正数的数列an、bn(n∈N*)中,已知an、bn2、an+1成等差数列,并且bn2、an+1、bn+12成等比数列.
(Ⅰ)证明:数列bn是等差数列;
(Ⅱ)若a1=2,a2=6,设cn=(an-n2)•qbn(q>0为常数),求数列cn的前n项和Sn
(Ⅰ)证明:数列bn是等差数列;
(Ⅱ)若a1=2,a2=6,设cn=(an-n2)•qbn(q>0为常数),求数列cn的前n项和Sn
(I)由题意知
,
又∵数列an、bn各项都是正数,∴an+1=bnbn+1,则an=bn-1bn
代入2bn2=an+an+1,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1,所以数列bn是等差数列.
(II)∵a1=2,a2=6,又2bn2=an+an+1,得2b12=a1+a2=8,解得b1=2
又∵a2=b1b2=6∴b2=3,由(I)知数列bn是等差数列,则公差d=b2-b1=1
∴bn=b1+(n-1)d=2+n-1=n+1,
又an=bn-1bn,得an=n(n+1)=n2+n,
∴cn=(an-n2)•qbn=nqn+1,
则当q=1时,cn=n,此时Sn=
;
当q≠1时,Sn=c1+c2++cn=1×q2+2×q3++nqn+1,①
所以qSn=qc1+qc2++qcn=1×q3+2×q4++nqn+2②
由①-②,得(1-q)Sn=q2+q3+qn+1-nqn+2=
-nqn+2,
即Sn=
-
综上可知,Sn=
|
又∵数列an、bn各项都是正数,∴an+1=bnbn+1,则an=bn-1bn
代入2bn2=an+an+1,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1,所以数列bn是等差数列.
(II)∵a1=2,a2=6,又2bn2=an+an+1,得2b12=a1+a2=8,解得b1=2
又∵a2=b1b2=6∴b2=3,由(I)知数列bn是等差数列,则公差d=b2-b1=1
∴bn=b1+(n-1)d=2+n-1=n+1,
又an=bn-1bn,得an=n(n+1)=n2+n,
∴cn=(an-n2)•qbn=nqn+1,
则当q=1时,cn=n,此时Sn=
| n(n+1) |
| 2 |
当q≠1时,Sn=c1+c2++cn=1×q2+2×q3++nqn+1,①
所以qSn=qc1+qc2++qcn=1×q3+2×q4++nqn+2②
由①-②,得(1-q)Sn=q2+q3+qn+1-nqn+2=
| q2(1-qn) |
| 1-q |
即Sn=
| q2(1-qn) |
| (1-q)2 |
| nqn+2 |
| 1-q |
综上可知,Sn=
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在各项均为正数的等比数列{ }中,
}中,  、
、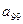 是方程
是方程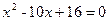 的两个根,则
的两个根,则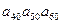 的值为
的值为
| A.32 | B.64 | C. 64 64 | D.256 |
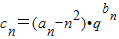 (q>0为常数),求数列cn的前n项和Sn
(q>0为常数),求数列cn的前n项和Sn