题目内容

S=1+
1
2
+
1
3
+…+
1
1000000
，则S的整数部分是（　　）
分析：利用放缩法进行放缩，S=1+
1
2
+
1
3
+
1
4
+…+
1
1000000
=1+
2
2
+
2
+
2
3
+
3
+…+
2
1000000
+
1000000
＜1+2×（
1
2
+1
+
1
3
+
2
+…+
2
1000000
+
999999
）=1999；
S＞1+
1
2
+
1
3
+
1
4
+…+
1
1000000
=
2
1
+
1
+
2
2
+
2
+
2
3
+
3
+…+
2
1000000
+
1000000
＞
2
2
+
1
+
2
3
+
2
+
2
4
+
3
+…+
2
1000000
+
999999
=1998．即1998＜S＜1999．从而得出S的整数部分．
解答：解：S=1+
1
2
+
1
3
+
1
4
+…+
1
1000000

=1+
2
2
+
2
+
2
3
+
3
+…+
2
1000000
+
1000000

＜1+2×（
1
2
+1
+
1
3
+
2
+…+
2
1000000
+
999999
）
=1+2×[
2
-1）+（
3
-
2
）+…+（
1000000
-
999999
]
=1+2×（-1+
1000000
）
=1+2×（1000-1）
=1999．
即S＜1999，
又∵S＞1+
1
2
+
1
3
+
1
4
+…+
1
1000000

=
2
1
+
1
+
2
2
+
2
+
2
3
+
3
+…+
2
1000000
+
1000000

＞
2
2
+
1
+
2
3
+
2
+
2
4
+
3
+…+
2
1000000
+
999999

=2×[（
2
-1）+（
3
-
2
）+（
4
-
3
）+…+（
1000000
-
999999
）]
=2×（-1+
1000000
）
=2×（1000-1）
=1998．
即s＞1998．
所以1998＜S＜1999．
所以S的整数部分1998．
故选B．
点评：本题考查放缩法、有理数域的解法，解题时要认真审题，注意挖掘题设中的隐含条件，合理地运用放缩法进行求解．
练习册系列答案
相关题目
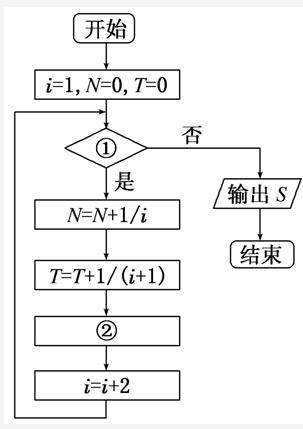精英家教网如图给出的是计算S=1-
1
2
+
1
3
-
1
4
+…+
1
99
-
1
100
的程序框图，请填充框图内所缺的式子，并写出程序．
如图给出的是计算S=1+
1
2
+
1
3
+…+
1
n
值的一个程序框图，当程序结束时，n的值为
2013
2013
．
对任意正整数n，设计一个程序求s=1+
1
2
+
1
3
+…+
1
n
的值．
若S=1+
1
2
+
1
3
+…+
1
1000000
，则S的整数部分是
1998
1998
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网