Question

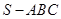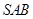在正三棱锥中，侧面、侧面、侧面两两垂直，且侧棱
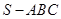，则正三棱锥外接球的表面积为____________.

Answer 1

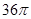
解析试题分析：∵正三棱锥S-ABC中，侧面SAB,侧面SAC,侧面SBC两两互相垂直
∴△SAB、△SAC、△SBC是等腰直角三角形，所以AB=BC=CA=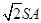=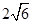,故该正三棱锥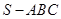外接球可以转换为正方体的外接球的表面积，根据边长求求解得到半径为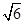，因此可知球的表面积为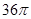
考点：本试题考查了球的表面积。
点评：利用等价转化的思想，借助于正方体的外接球的表面积来求解正三棱锥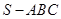外接球的表面积，是解题的关键，属于中档题。