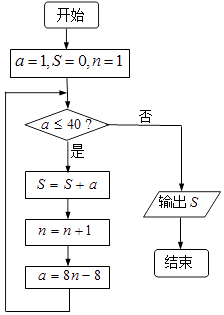
题目内容
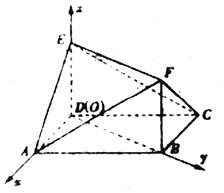
【题目】如图所示的多面体中,ABCD是平行四边形,BDEF是矩形,ED⊥面ABCD,∠ABD= ![]() ,AB=2AD.
,AB=2AD. 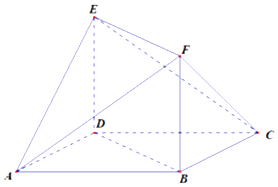
(Ⅰ)求证:平面BDEF⊥平面ADE;
(Ⅱ)若ED=BD,求AF与平面AEC所成角的正弦值.
【答案】(Ⅰ)证明:设AD=a,AD=2a,∠ABD= ![]() , ∴cos∠ABD=
, ∴cos∠ABD= ![]() =
= ![]() ,解得BD=
,解得BD= ![]() a,
a,
∴BD2+AD2=AB2 , 即BD⊥AD.
∵DE⊥平面ABCD,BD平面ABCD,
∴DE⊥BD,又AD∩DE=D,AD平面ADE,DE平面ADE,
∴BD⊥平面ADE,又BD平面BDEF,
∴平面BDEF⊥平面ADE.
(Ⅱ)解:由(Ⅰ)AD⊥BD,BD= ![]() AD,
AD,
以D为坐标原点,以射线DA,DB,DE分别为x轴,y轴,z轴正方向的空间直角坐标系,如图所示:
设AD=1,则A(1,0,0), ![]() ,
, ![]() ,
, ![]() .
.![]() =(﹣1,0,
=(﹣1,0, ![]() ),
), ![]() =(﹣2,
=(﹣2, ![]() ,0),
,0), ![]() ,
,
设平面AEC的法向量为 ![]() ,则
,则 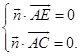 ,∴
,∴  ,
,
令z=1,得 ![]() ,
,
∴ 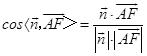 =
= ![]() =
= ![]() .
.
所以直线AF与平面AEC所成角的正弦值为 ![]() .
.
【解析】(Ⅰ)利用余弦定理得出BD= ![]() AD,由勾股定理即可得出AD⊥BD,再由DE⊥平面ABCD得出DE⊥BD,从而有BD⊥ADE,故平面BDEF⊥平面ADE;(Ⅱ)建立空间坐标系,求出平面AEC的法向量
AD,由勾股定理即可得出AD⊥BD,再由DE⊥平面ABCD得出DE⊥BD,从而有BD⊥ADE,故平面BDEF⊥平面ADE;(Ⅱ)建立空间坐标系,求出平面AEC的法向量 ![]() ,计算
,计算 ![]() 与
与 ![]() 的夹角即可得出线面角的大小.
的夹角即可得出线面角的大小.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

【题目】某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2. 表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.