题目内容
已知正四棱锥S-ABCD的所有棱长均为
,则过该棱锥的顶点S及底面正方形各边中点的球的体积为 .
| 2 |
分析:设球半径为R,底面中心为O'且球心为O.正四棱锥S-A′B′C′D′中A′B′=1,SA′=
,算出SO′=1,OO'=SO'-SO=1-R,在Rt△AOO′中利用勾股定理建立关于R的等式,解出R,再利用球的体积公式即可得到外接球的体积.
| ||
| 2 |
解答: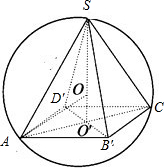 解:如图所示,设球半径为R,底面中心为O'且球心为O,
解:如图所示,设球半径为R,底面中心为O'且球心为O,
∵正四棱锥S-A′B′C′D′中A′B′=1,SA′=
,
∴A′O′=
,可得SO′=1,OO'=SO'-SO=1-R.
∵在Rt△A′OO'中,A′O2=A′O'2+OO'2,
∴R2=(
)2+(1-R)2,解之得R=
,
因此可得外接球的体积V=
πR3=
π.
故答案为:
π.
 解:如图所示,设球半径为R,底面中心为O'且球心为O,
解:如图所示,设球半径为R,底面中心为O'且球心为O,∵正四棱锥S-A′B′C′D′中A′B′=1,SA′=
| ||
| 2 |
∴A′O′=
| ||
| 2 |
∵在Rt△A′OO'中,A′O2=A′O'2+OO'2,
∴R2=(
| ||
| 2 |
| 3 |
| 4 |
因此可得外接球的体积V=
| 4 |
| 3 |
| 9 |
| 16 |
故答案为:
| 9 |
| 16 |
点评:本题给出正四棱锥的形状,求它的外接球的体积,着重考查了正棱锥的性质、多面体的外接球、勾股定理与球的体积公式等知识,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
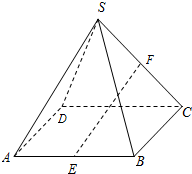 (文做理不做)已知:正四棱锥S-ABCD的高为
(文做理不做)已知:正四棱锥S-ABCD的高为