题目内容
(理科做)设f(n)=1+
+
+…+
,用数学归纳法证明:当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n).
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
10、当n=2时,等式左边=2+f(1)=2+1=3
等式右边=2f(2)=2(1+
)=3,∴原式成立;…(4分)
20、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
∵f(n)=1+
+
+…+
,∴f(n+1)=f(n)+
(这步可置于后)…(8分)
则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=(k+1)f(k)+1=(k+1)[f(k)+
]=(k+1)f(k+1)
即当n=k+1时,等式也成立.…(12分)
综上10,20可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立
…(14分)
等式右边=2f(2)=2(1+
| 1 |
| 2 |
20、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
∵f(n)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=(k+1)f(k)+1=(k+1)[f(k)+
| 1 |
| k+1 |
即当n=k+1时,等式也成立.…(12分)
综上10,20可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立
…(14分)

练习册系列答案
相关题目
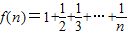 ,用数学归纳法证明:当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n).
,用数学归纳法证明:当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n).