题目内容
(理科做)设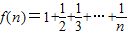 ,用数学归纳法证明:当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n).
,用数学归纳法证明:当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n).
【答案】分析:分析:首先题目要求应用数学归纳法证明不等式,数学归纳法的一般步骤是,第一步验证第一项是否成立,第二步假设n=k时候结论成立,去验证n=k+1时候结论是否成立.若都成立即得证.
解答:解:1、当n=2时,等式左边=2+f(1)=2+1=3
等式右边=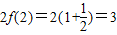 ,∴原式成立;…(4分)
,∴原式成立;…(4分)
2、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
∵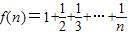 ,∴
,∴ (这步可置于后)…(8分)
(这步可置于后)…(8分)
则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=
即当n=k+1时,等式也成立.…(12分)
综上1,2可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立
…(14分)
点评:点评:此题主要考查数列的递推公式和利用数学归纳法进行证明,归纳法是高考中常考的方法,几乎每年都考,对此学生要引起注意,多加练习.
解答:解:1、当n=2时,等式左边=2+f(1)=2+1=3
等式右边=
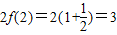 ,∴原式成立;…(4分)
,∴原式成立;…(4分)2、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
∵
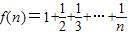 ,∴
,∴ (这步可置于后)…(8分)
(这步可置于后)…(8分)则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=

即当n=k+1时,等式也成立.…(12分)
综上1,2可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立
…(14分)
点评:点评:此题主要考查数列的递推公式和利用数学归纳法进行证明,归纳法是高考中常考的方法,几乎每年都考,对此学生要引起注意,多加练习.

练习册系列答案
相关题目