题目内容
15.过抛物线y2=2px(p>0)的焦点F的一条直线交抛物线于点P、Q,设点Q关于x轴的对称点为Q′,准线与X轴的交点是点B,求证:P、Q′、B三点共线.分析 如图所示,设P$(\frac{{y}_{1}^{2}}{2p},{y}_{1})$,Q$(\frac{{y}_{2}^{2}}{2p},{y}_{2})$,${Q}^{′}(\frac{{y}_{2}^{2}}{2p},-{y}_{2})$,B$(-\frac{p}{2},0)$.利用斜率计算公式可得:${k}_{P{Q}^{′}}$,kPB.设直线PQ的方程为:$my+\frac{p}{2}$=x,与抛物线方程联立化为y2-2pmy-p2=0,可得根与系数的关系,只有证明kPB=${k}_{P{Q}^{′}}$,即可得出.
解答 证明:如图所示,
设P$(\frac{{y}_{1}^{2}}{2p},{y}_{1})$,Q$(\frac{{y}_{2}^{2}}{2p},{y}_{2})$,${Q}^{′}(\frac{{y}_{2}^{2}}{2p},-{y}_{2})$,B$(-\frac{p}{2},0)$.
${k}_{P{Q}^{′}}$=$\frac{{y}_{1}+{y}_{2}}{\frac{{y}_{1}^{2}}{2p}-\frac{{y}_{2}^{2}}{2p}}$=$\frac{2p}{{y}_{1}-{y}_{2}}$,kPB=$\frac{{y}_{1}}{\frac{{y}_{1}^{2}}{2p}+\frac{p}{2}}$=$\frac{2p{y}_{1}}{{y}_{1}^{2}+{p}^{2}}$.
设直线PQ的方程为:$my+\frac{p}{2}$=x,
联立$\left\{\begin{array}{l}{my+\frac{p}{2}=x}\\{{y}^{2}=2px}\end{array}\right.$,化为y2-2pmy-p2=0,
∴y1y2=-p2.
∴kPB=$\frac{2p{y}_{1}}{{y}_{1}^{2}+{p}^{2}}$=$\frac{2p{y}_{1}}{{y}_{1}^{2}-{y}_{1}{y}_{2}}$=$\frac{2p}{{y}_{1}-{y}_{2}}$,
∴kPB=${k}_{P{Q}^{′}}$,
∴P、Q′、B三点共线.
点评 本题考查了抛物线的定义及其性质、过焦点的弦的性质、直线与抛物线相交转化为方程联立可得根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于中档题.

| A. | 0 | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
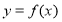 的导函数
的导函数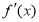 的图象,则下面判断正确的是( )
的图象,则下面判断正确的是( )
 上
上 是增函数 B.当
是增函数 B.当 时,
时, 取极大值
取极大值 上
上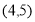 上
上 ,若
,若 ,则
,则 的范围是 .
的范围是 .