题目内容
给定命题 :
:
 是无理数
是无理数 ,
, 是无理数;命题
是无理数;命题 :已知非零向量
:已知非零向量 、
、 ,则“
,则“ ”是“
”是“ ”的充要条件.则下列各命题中,假命题是( )
”的充要条件.则下列各命题中,假命题是( )
A. | B. | C. | D. |
D
解析试题分析: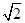 是无理数,但
是无理数,但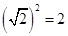 是有理数,所以p是假命题. 由向量的平行四边形法则,若两向量满足
是有理数,所以p是假命题. 由向量的平行四边形法则,若两向量满足 ,则两向量垂直.所以q是真命题,根据逻辑联结词的意义:
,则两向量垂直.所以q是真命题,根据逻辑联结词的意义: 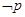 是真命题,
是真命题,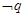 是假命题.
是假命题.
考点:逻辑联结词,简单的复合命题的真假判定.

练习册系列答案
相关题目
下列说法正确的是( )
A.“ ”是“函数 ”是“函数 是奇函数”的充要条件 是奇函数”的充要条件 |
B.若 , , ,则 ,则  , , |
C.若 为假命题,则p,q均为假命题 为假命题,则p,q均为假命题 |
D.“若 ,则 ,则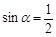 ”的否命题是“若 ”的否命题是“若 ,则 ,则 ” ” |
命题甲: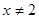 或
或 ;命题乙:
;命题乙: ,则甲是乙的( )
,则甲是乙的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既不充分条件也不必要条件 |
“函数 有零点”的充要条件是( )
有零点”的充要条件是( )
A. | B. | C. | D. |
“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要的条件 |
已知向量 ,
,  ,则
,则 是
是 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若p: ,q:f(x)=sin(
,q:f(x)=sin( )(
)( )是偶函数,则p是q的( )
)是偶函数,则p是q的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
 在R上为增函数,p2:函数
在R上为增函数,p2:函数 在R上为减函数,则在命题
在R上为减函数,则在命题 和
和 中,真命题是 ( )
中,真命题是 ( )


