题目内容
(上海春卷4)已知集合A={x||x|<2},B={x|| 1 | x+1 |
分析:由题意先求出不等式的解集,再表示出集合A、B,再求出它们的交集.
解答:解:解|x|<2得,-2<x<2;
解x+1>0得,x>-1;
∴A={x|-2<x<2},B={x|x>-1},
故A∩B={x|-1<x<2}.
故答案为:{x|-1<x<2}.
解x+1>0得,x>-1;
∴A={x|-2<x<2},B={x|x>-1},
故A∩B={x|-1<x<2}.
故答案为:{x|-1<x<2}.
点评:本题考查了交集的运算,对于较复杂并含有不等式的集合可借助于数轴.

练习册系列答案
相关题目
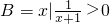 ,则A∩B=________.
,则A∩B=________.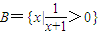 ,则A∩B=______.
,则A∩B=______.