题目内容
动点P(x,y)在线段AB上移动,其中A(-3,0),B(0,3),求:
(1)
的取值范围;
(2)
+
的最小值及此时P点的坐标.
(1)
| y+1 |
| x-1 |
(2)
| x2+y2 |
| (x-1)2+y2 |
分析:(1)根据直线的倾斜公式,设C(1,-1)得
表示PC的斜率.由此作出图形并观察PC倾斜角的变化,即可得到
的取值范围;
(2)设M(0,0),N(1,0),则所求目标函数表示P与M、N两点间的距离之和.利用点关于直线对称的方法进行求解,即可得到当P点的坐标为(-
,
)时,目标函数的最小值为5.
| y+1 |
| x-1 |
| y+1 |
| x-1 |
(2)设M(0,0),N(1,0),则所求目标函数表示P与M、N两点间的距离之和.利用点关于直线对称的方法进行求解,即可得到当P点的坐标为(-
| 9 |
| 7 |
| 12 |
| 7 |
解答:解:(1)设C(1,-1),则
=kPC,表示PC的斜率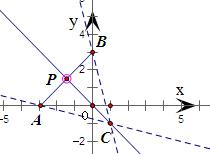
观察图形,直线PA的倾斜角总是钝角,由此可得
当P与A重合时,kPC=-
达到最大值;
当P与B重合时,kPC=-4达到最小值
∴kPC∈[-4,-
],即-4≤
≤-
(2)直线AB的方程为lAB:x-y+3=0,
设M(0,0),N(1,0),M'为点M关于直线AB对称的点,
求得M'(-3,3),则|PM|+|PN|=
+
∵|PM|+|PN|=|PM′|+|PN|≥|M′N|
∴当P、M'、N三点共线时,
|PM|+|PN|达到最小值|M′N|=
=5
求得直线M′N方程为3x+4y-3=0,
由此解出M′N、AB的交点坐标为P(-
,
)
∴
+
的最小值等于5,此时P点的坐标为(-
,
).
| y+1 |
| x-1 |

观察图形,直线PA的倾斜角总是钝角,由此可得
当P与A重合时,kPC=-
| 1 |
| 4 |
当P与B重合时,kPC=-4达到最小值
∴kPC∈[-4,-
| 1 |
| 4 |
| y+1 |
| x-1 |
| 1 |
| 4 |
(2)直线AB的方程为lAB:x-y+3=0,
设M(0,0),N(1,0),M'为点M关于直线AB对称的点,
求得M'(-3,3),则|PM|+|PN|=
| x2+y2 |
| (x-1)2+y2 |
∵|PM|+|PN|=|PM′|+|PN|≥|M′N|
∴当P、M'、N三点共线时,
|PM|+|PN|达到最小值|M′N|=
| (-3-1)2+(3-0)2 |
求得直线M′N方程为3x+4y-3=0,
由此解出M′N、AB的交点坐标为P(-
| 9 |
| 7 |
| 12 |
| 7 |
∴
| x2+y2 |
| (x-1)2+y2 |
| 9 |
| 7 |
| 12 |
| 7 |
点评:本题给出线段AB,求直线斜率的范围并求距离和的最小值.着重考查了直线的基本量与基本形式、点关于直线对称和两点的距离公式等知识,属于基础题.

练习册系列答案
相关题目
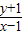 的取值范围;
的取值范围; 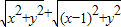 的最小值及此时P点的坐标.
的最小值及此时P点的坐标.