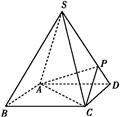
题目内容
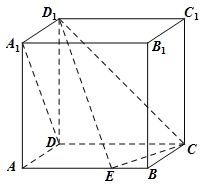
如图,在四棱锥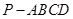 中,底面
中,底面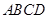 是边长为1的菱形,
是边长为1的菱形,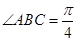 ,
, 底面
底面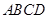 ,
,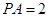 ,
,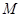 为
为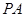 的中点,
的中点,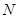 为
为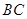 的中点,
的中点,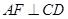 于
于 ,如图建立空间直角坐标系.
,如图建立空间直角坐标系.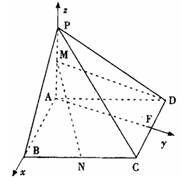
(1)求出平面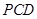 的一个法向量并证明
的一个法向量并证明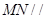 平面
平面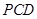 ;
;
(2)求二面角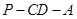 的余弦值.
的余弦值.
(1)证明详见解析;(2)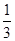 .
.
解析试题分析:这是一道应用空间向量解决空间平行与空间角问题的试题.(1)先确定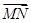 、
、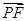 、
、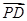 的坐标,然后设出平面
的坐标,然后设出平面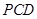 的一个法向量为
的一个法向量为 ,由
,由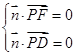 确定
确定 的一个取值,最后验证
的一个取值,最后验证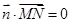 ,即可作出
,即可作出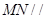 平面
平面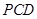 的判断;(2)先找到
的判断;(2)先找到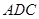 的一个法向量为
的一个法向量为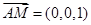 ,然后计算
,然后计算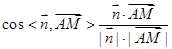 ,最后结合图形,确定二面角
,最后结合图形,确定二面角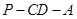 的余弦值是
的余弦值是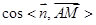 ,还是
,还是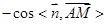 .
.
试题解析:由题设知:在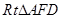 中,
中,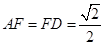

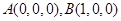 、
、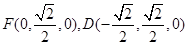 、
、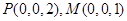 、
、 4分
4分
(1)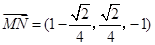 5分
5分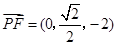 ,
,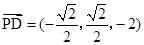 6分
6分
设平面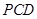 的一个法向量为
的一个法向量为
则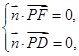

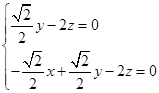
令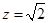 ,得
,得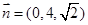 8分
8分
∵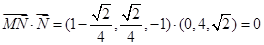
∴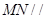 平面
平面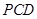 10分
10分
(2)由(1)得平面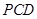 的法向量
的法向量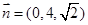 ,平面
,平面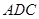 的一个法向量为
的一个法向量为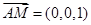 12分
12分
设二面角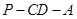 的平面角为
的平面角为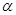 ,则
,则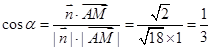
即二面角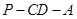 的余弦值为
的余弦值为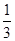 14分.
14分.
考点:1.空间向量的解决空间平行中的应用;2.空间向量在解决空间角中的应用.

练习册系列答案
相关题目
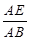 的值;
的值;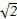 ,☉O的直径AB=2,C是
,☉O的直径AB=2,C是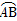 的中点,D为AC的中点.
的中点,D为AC的中点.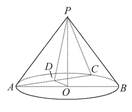
 ·
· .
. ,E是PB上任意一点.
,E是PB上任意一点.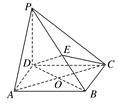
 ,若E为PB的中点,求EC与平面PAB所成角的正弦值.
,若E为PB的中点,求EC与平面PAB所成角的正弦值.
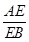 =
=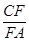 =
=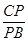 =
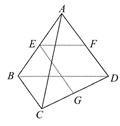
= (如图(1)),将△AEF沿EF折起到△
(如图(1)),将△AEF沿EF折起到△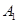 EF的位置,使二面角
EF的位置,使二面角 EF
EF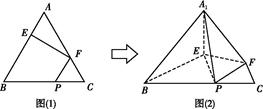

 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的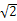 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.