题目内容
(08年华师一附中二次压轴文)某工厂计划生产甲、乙两种畅销产品,甲、乙的加工过程必须经过A、B两个生产环节,甲产品在A、B两个环节所需时间分别为1小时和2小时,乙产品在A、B两个环节所需时间分别为2小时和1小时,而A、B两个生产环节在一个月内生产总时数不超过400小时和500小时,如果甲、乙两种产品销售单价分别为3千元/件,2千元/件。问在一个月内,甲、乙两种产品各生产多少件能使该厂销售收入最多?
解析:设甲、乙两种产品的产量分别为x,y件,约束条件是
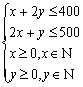
目标函数是z=3x+2y,画出可行域,如图。
使3x+2y取得最大值的(x,y)是两直线2x+y=500与x+2y=400的交点(200,100)。
甲、乙两种产品的每月产量分别为200、100件时,可得最大收入800千元。


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
