题目内容
已知在同一平面内 满足条件:
满足条件: =
= ,
,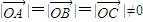 .
.(I)求证:△ABC为正三角形;
(II)类比于(I),在同一平面内,若向量
 满足条件:
满足条件: =
=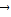 ,
,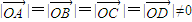 ,试判断四边形ABCD的形状,并给予证明.
,试判断四边形ABCD的形状,并给予证明.
【答案】分析:(I)利用向量的运算法则将等式中的向量 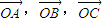 用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状.
用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状.
(II)先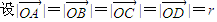 ,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又
,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又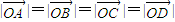 得出四边形ABCD为矩形.
得出四边形ABCD为矩形.
解答:解: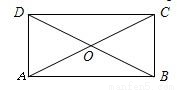 (I)证明:设
(I)证明:设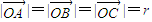
则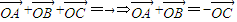
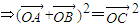
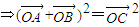
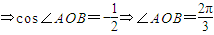 (3分)
(3分)

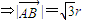
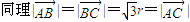
∴△ABC为正三角形(6分)
(II)四边形ABCD为矩形(8分)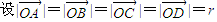 ,则
,则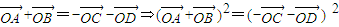 ⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD
⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD
同理∠AOD=∠BOC(10分)
又∠AOB+∠BOC+∠COD+∠DOA=360°
∴∠AOD+∠COD=180°即A、O、C三点共线
同理B、O、D三点共线又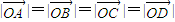
∴四边形ABCD为矩形.(12分)
点评:本题考查向量的运算法则及利用向量判断出三角形的形状.解答的基础是对向量运算和变形的熟悉掌握.
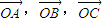 用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状.
用三角形的各边对应的向量表示,得到边的关系,得出三角形的形状.(II)先
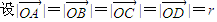 ,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又
,根据向量的运算得出:∠AOB=∠COD;∠AOD=∠BOC从而∠AOD+∠COD=180°即A、O、C三点共线及、O、D三点共线,又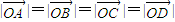 得出四边形ABCD为矩形.
得出四边形ABCD为矩形.解答:解:
 (I)证明:设
(I)证明:设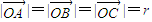
则
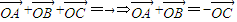
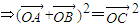
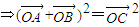
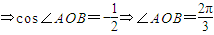 (3分)
(3分)

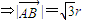
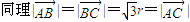
∴△ABC为正三角形(6分)
(II)四边形ABCD为矩形(8分)
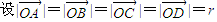 ,则
,则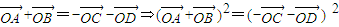 ⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD
⇒2r2+2r2cos∠AOB=2r2+2r2cos∠COD⇒∠AOB=∠COD同理∠AOD=∠BOC(10分)
又∠AOB+∠BOC+∠COD+∠DOA=360°
∴∠AOD+∠COD=180°即A、O、C三点共线
同理B、O、D三点共线又
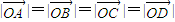
∴四边形ABCD为矩形.(12分)
点评:本题考查向量的运算法则及利用向量判断出三角形的形状.解答的基础是对向量运算和变形的熟悉掌握.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 满足条件:
满足条件: ,
, 。
。 满足条件:
满足条件: ,
, ,试判断四边形ABCD的形状,并给予证明。
,试判断四边形ABCD的形状,并给予证明。  |=2a(a>0),动点P与F1、F2在同一平面内,且满足|
|=2a(a>0),动点P与F1、F2在同一平面内,且满足|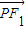 +
+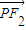 |=4a,则动点P的轨迹是( )
|=4a,则动点P的轨迹是( )