题目内容
计算下列各式
(1)32+log32-5
+(
×
)4-(0.0643)-
;
(2)(lg2)2+lg5•lg20-1.
(1)32+log32-5
| 1 |
| log4925 |
| 2 |
| 4 | 3 |
| 1 |
| 9 |
(2)(lg2)2+lg5•lg20-1.
分析:(1)根据对数恒等式进行化简和把底数写成乘方的形式,然后根据幂的乘方的运算法则化简可得值;
(2)利用对数的运算性质lga•b=lga+lgb化简得到.
(2)利用对数的运算性质lga•b=lga+lgb化简得到.
解答:解:(1)32+log32-5
+(
×
)4-(0.0643)-
=9×2-7+4×3-
=20.5
(2)原式=(lg2)2+(2lg2+lg5)lg5-1=(lg2+lg5)2-1=0
| 1 |
| log4925 |
| 2 |
| 4 | 3 |
| 1 |
| 9 |
=9×2-7+4×3-
| 5 |
| 2 |
=20.5
(2)原式=(lg2)2+(2lg2+lg5)lg5-1=(lg2+lg5)2-1=0
点评:考查学生灵活运用对数运算性质来化简求值,学会利用幂的乘方法则对分数指数进行化简计算.

练习册系列答案
相关题目
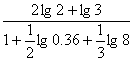 ;?
;? b
b )(-3a
)(-3a )÷(
)÷( a
a b
b )
)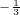 -(-
-(- )-2+(44)
)-2+(44) -3-1+(
-3-1+( -1)0.
-1)0.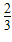 b
b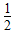 )(-3a
)(-3a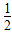 b
b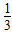 )÷(
)÷( a
a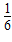 b
b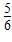 )
)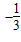 -(-
-(- )-2+(44)
)-2+(44)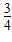 -3-1+(
-3-1+(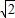 -1).
-1).