题目内容
如图,平面EFGH分别平行于CD、AB,E、F、G、H分别在BD、BC、AC、AD上,并且CD=a,AB=b,CD⊥AB.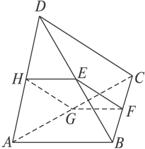
(1)求证:四边形EFGH是矩形;
(2)点E在什么位置时,矩形EFGH的面积最大?
(1)证明:∵CD∥平面EFGH,平面EFGH∩平面BCD=EF,
∴CD∥EF.
同理,HG∥CD,
∴EF∥HG.
同理,HE∥GF,
∴四边形EFGH为平行四边形.
∵CD∥EF,HE∥AB,
∴∠HEF为AB和CD所成的角.
∵CD⊥AB,
∴HE⊥EF.
∴四边形EFGH为矩形.
(2)解析:由(1)可知在△BCD中,EF∥CD,
设DE=m,EB=n,则![]() .
.
∴EF=![]() a.
a.
同理,HE=![]() b.
b.
∵四边形EFGH为矩形,
∴S矩形EFGH=HE·EF=![]() .
.
∵m+n≥![]() ,
,
∴(m+n)2≥4mn.
∴![]() (当且仅当m=n时取“=”,即E为BD的中点时“=”成立).
(当且仅当m=n时取“=”,即E为BD的中点时“=”成立).
∴当E为BD的中点时,(S矩形EFGH)max=![]() ab.
ab.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 6、如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH上及其内部运动,则M满足条件
6、如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH上及其内部运动,则M满足条件

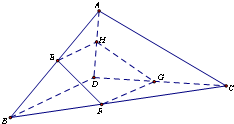 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.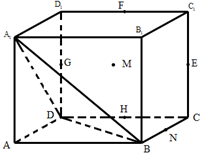 如图,在边长为a的正方体ABCD-A1B1C1D1中,E,F,G,H分别是CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上及其内部运动,若MN∥平面A1BD,则点M轨迹的长度是
如图,在边长为a的正方体ABCD-A1B1C1D1中,E,F,G,H分别是CC1,C1D1,D1D,CD的中点,N是BC的中点,M在四边形EFGH上及其内部运动,若MN∥平面A1BD,则点M轨迹的长度是 如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.
如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.