题目内容
已知集合A={-2,0,2},B={-1,1}.
(Ⅰ)若M={(x,y)|x∈A,y∈B},用列举法表示集合M;
(Ⅱ)在(Ⅰ)中的集合M内,随机取出一个元素(x,y),求以(x,y)为坐标的点位于区域D: 内的概率.
内的概率.
解:(Ⅰ)M={(-2,-1),(-2,1),(0,-1),(0,1),(2,-1),(2,1)}.(6分)
(Ⅱ)记“以(x,y)为坐标的点位于区域D内”为事件A.
集合M中共有6个元素,即基本事件总数为6,区域D含有集合M中的元素4个,
所以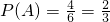 .故以(x,y)为坐标的点位于区域D内的概率为
.故以(x,y)为坐标的点位于区域D内的概率为 .(13分)
.(13分)
分析:(I)直接列举即可
(II)由(I)可先求满足条件的集合M中的元素个数,把所有元素分别代入到区域D所满足的不等式組求出区域D含有集合M中的元素,代入古典概率的计算公式可求
点评:本题是古典概率的计算公式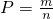 的简单运用,属于基础试题.解题的关键是要准确、全面的找出公式中的m,n的值.
的简单运用,属于基础试题.解题的关键是要准确、全面的找出公式中的m,n的值.
(Ⅱ)记“以(x,y)为坐标的点位于区域D内”为事件A.
集合M中共有6个元素,即基本事件总数为6,区域D含有集合M中的元素4个,
所以
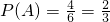 .故以(x,y)为坐标的点位于区域D内的概率为
.故以(x,y)为坐标的点位于区域D内的概率为 .(13分)
.(13分)分析:(I)直接列举即可
(II)由(I)可先求满足条件的集合M中的元素个数,把所有元素分别代入到区域D所满足的不等式組求出区域D含有集合M中的元素,代入古典概率的计算公式可求
点评:本题是古典概率的计算公式
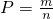 的简单运用,属于基础试题.解题的关键是要准确、全面的找出公式中的m,n的值.
的简单运用,属于基础试题.解题的关键是要准确、全面的找出公式中的m,n的值. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目