题目内容
设M(k)是满足不等式log25x+log25(26×25k-1-x)≥2k-1的正整数x的个数,记S=M(1)+M(2)+…+M(n) n∈N.
(1)求S;
(2)设t=5n-2+5n+2+n-2 (n∈N),试比较S与t的大小.
解:(1)化简得 x2-26•25k-1x+252k-1≤0
∴25k-1≤x≤25k …
∴M(k)=25k-25k-1+1 …
S=(251-250+1)+(252-251+1)+…+(25n-25n-1+1)=25n+n-1…
(2)要S-t=(52n- …
…
只要 5n>25或5n<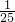
即:n>2或n<-2 …
∴当n>2 时s>t;当n=2时s=t; 当n=1时s<t …
分析:(1)先将原不等式化简得x2-26•25k-1x+252k-1≤0,利用换元法解出x的范围,从而得出正整数x的个数M(k)=25k-25k-1+1 再利用等比数列的求和公式求得S=(251-250+1)+(252-251+1)+…+(25n-25n-1+1)即可;
(2)因S-t=(52n- ,只要 5n>25或5n<
,只要 5n>25或5n<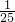 ,求得其等价的条件,从而得出S与t的大小与相应的n的值.
,求得其等价的条件,从而得出S与t的大小与相应的n的值.
点评:本小题主要考查函数单调性的应用、对数函数图象与性质的综合应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
∴25k-1≤x≤25k …
∴M(k)=25k-25k-1+1 …
S=(251-250+1)+(252-251+1)+…+(25n-25n-1+1)=25n+n-1…
(2)要S-t=(52n-
 …
…只要 5n>25或5n<
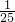
即:n>2或n<-2 …
∴当n>2 时s>t;当n=2时s=t; 当n=1时s<t …
分析:(1)先将原不等式化简得x2-26•25k-1x+252k-1≤0,利用换元法解出x的范围,从而得出正整数x的个数M(k)=25k-25k-1+1 再利用等比数列的求和公式求得S=(251-250+1)+(252-251+1)+…+(25n-25n-1+1)即可;
(2)因S-t=(52n-
 ,只要 5n>25或5n<
,只要 5n>25或5n<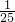 ,求得其等价的条件,从而得出S与t的大小与相应的n的值.
,求得其等价的条件,从而得出S与t的大小与相应的n的值.点评:本小题主要考查函数单调性的应用、对数函数图象与性质的综合应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
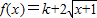 是递增闭函数,则实数k的取值范围是( )
是递增闭函数,则实数k的取值范围是( )