题目内容
“0＜a＜b”是“(
)a＞(
)b”的（ ）
| 1 |
| 4 |
| 1 |
| 4 |
分析：根据底数大于0小于1的指数函数在R上为减函数，先判断“0＜a＜b”⇒“(
)a＞(
)b”的真假，与“(
)a＞(
)b”⇒“0＜a＜b”的真假，然后根据充要条件的定义得到结论．
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答：解：当“0＜a＜b”时，“(
)a＞(
)b”成立，故“0＜a＜b”是“(
)a＞(
)b”的充分条件；
当“(
)a＞(
)b”时，“a＜b”成立，但“0＜a＜b”不一定成立，故“0＜a＜b”是“(
)a＞(
)b”的不必要条件
故“0＜a＜b”是“(
)a＞(
)b”充分不必要条件
故选A
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当“(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
故“0＜a＜b”是“(
| 1 |
| 4 |
| 1 |
| 4 |
故选A
点评：本题考查的知识点是充要条件的定义及指数函数的单调性，其中根据指数函数的单调性，判断“0＜a＜b”⇒“(
)a＞(
)b”的真假，与“(
)a＞(
)b”⇒“0＜a＜b”的真假，是解答本题的关键．
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
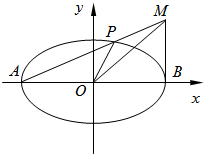如图，已知椭圆