题目内容
10．在△ABC中，a，b，c分别为角A、B、C的对边，且acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b，求证：B≤$\frac{π}{3}$．分析 已知等式利用二倍角的余弦函数公式化简，整理后利用正弦定理及两角和与差的正弦函数公式化简，再利用诱导公式变形得到关系式，再利用正弦定理化简得到a+c=2b，利用余弦定理表示出cosB，把得出关系式代入并利用基本不等式求出cosB≥$\frac{1}{2}$，利用余弦函数的性质判断即可得证．
解答 证明：在△ABC中，acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3}{2}$b，
整理得：$\frac{a（1+cosC）}{2}$+$\frac{c（1+cosA）}{2}$=$\frac{3}{2}$b，即a（1+cosC）+c（1+cosA）=3b，
利用正弦定理化简得：sinA（1+cosC）+sinC（1+cosA）=3sinB，
即sinA+sinC+sinAcosC+cosAsinC=sinA+sinC+sin（A+C）=sinA+sinC+sinB=3sinB，
整理得：sinA+sinC=2sinB，
再利用正弦定理化简得：a+c=2b，
由余弦定理得：cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-\frac{（a+c）^{2}}{4}}{2ac}$=$\frac{3}{8}$•$\frac{{a}^{2}+{c}^{2}}{ac}$-$\frac{1}{4}$≥$\frac{3}{4}$-$\frac{1}{4}$=$\frac{1}{2}$，
则B≤$\frac{π}{3}$．
点评 此题考查了正弦定理，余弦定理，以及基本不等式的运用，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
18．已知a＞0，“x∈{-a，a}”是“|x|=a”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 非充分非必要条件 |
2．
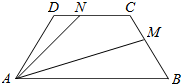在等腰梯形ABCD中，∠A=$\frac{π}{3}$，边AB、DC的长分别为2、1，若M、N分别是边BC、CD上的点，且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|，则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是（ ）
在等腰梯形ABCD中，∠A=$\frac{π}{3}$，边AB、DC的长分别为2、1，若M、N分别是边BC、CD上的点，且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|，则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是（ ）| A． | [$\frac{3}{2}$，+∞） | B． | （0，2] | C． | [$\frac{3}{2}$，3] | D． | （$\frac{3}{2}$，2） |