题目内容
过点M(1,1)作直线与抛物线x2=2y交于A、B两点,该抛物线在A、B两点处的两条切线交于点P.(I)求点P的轨迹方程;
(II)求△ABP的面积的最小值.
分析:(I)设出过点M(1,1)的直线y=k(x-1)+1与抛物线x2=2y联立,利用导数的几何意义表示切线斜率,将两条直线联立的交点坐标,再结合韦达定理消参即可
(II)将△ABP的边|AB|和点P到直线AB的距离用斜率K表示,利用三角形面积公式S=
=|AB|•d,即可计算求△ABP的面积的最小值
(II)将△ABP的边|AB|和点P到直线AB的距离用斜率K表示,利用三角形面积公式S=
| 1 |
| 2 |
解答:解:(I)设直线AB方程为由y=k(x-1)+1,
代入x2=2y,得x2-2kx+2k-2=0
则切线PA的方程为y=x1(x-x1)+
,即y=x1x-
.①
同理,切线PB的方程为y=x2x-
.②
由①、②两式得点P的坐标为(
,
),
于是P(k,k-1),即点P轨迹的参数方程为
消去参数k,得点P的轨迹方程为x-y-1=0.
(II)由(I)知
点P到直线AB的距离d=
=
,
△ABC的面积S=
|AB|•d=(k2-2k+2)
=[(k-1)2+1]
.
当k=1时,S有最小值1.
代入x2=2y,得x2-2kx+2k-2=0
|
则切线PA的方程为y=x1(x-x1)+
| ||
| 2 |
| ||
| 2 |
同理,切线PB的方程为y=x2x-
| ||
| 2 |
由①、②两式得点P的坐标为(
| x1+x2 |
| 2 |
| x1x2 |
| 2 |
于是P(k,k-1),即点P轨迹的参数方程为
|
消去参数k,得点P的轨迹方程为x-y-1=0.
(II)由(I)知
|
点P到直线AB的距离d=
| |k(k-1)+1-(k-1)| | ||
|
| k2-2k+2 | ||
|
△ABC的面积S=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当k=1时,S有最小值1.
点评:本题考查了直线与抛物线的关系,特别要注意韦达定理,设而不求解题思想的运用

练习册系列答案
相关题目


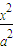 +
+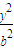 =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).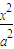 +
+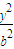 =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).