题目内容
设全集
.
（1）解关于x的不等式
;
（2）记A为(1)中不等式的解集，集合
，若
恰有3个元素，求
的取值范围.
（1）当
时，原不等式的解集为
；当
时，原不等式的解集为
；
（2）
．
解析试题分析：
解题思路：(1)讨论的范围，分情况求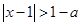
的解集即可；（2）先化简集合
,再利用题意得出
的限制条件，进而求的范围.
规律总结：解绝对值不等式的题型主要有：
，
；主要思路从去掉绝对值符号入手，往往讨论变量的范围去掉绝对值符号，变成分段函数求解问题.
试题解析：（1）∵
∴
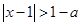
ⅰ当
即时，原不等式的解集为R
ⅱ当
即时，
或
∴
或
此时原不等式的解集为.
（2）
∵
恰有3个元素，∴，
∵ ∴
∴
∵恰有3个元素
∴
或
或
解得：
所以
的取值范围为.
考点：1.绝对值不等式；2.集合间的运算.
练习册系列答案
相关题目
，记和
中所有不同值的个数为
．如当
时，由
，
，
，
，
，得
．对于集合
，若实数
成等差数列，则
= ． 
，函数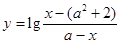
的定义域为集合B.
时，求集合
;
,命题q: 
,若q是p的必要条件，求实数a的取值范围.
，求实数m的值；
，求实数m的取值范围。
，B＝{x|m＋1≤x≤2m－1}．
的值域，集合C为不等式
(x＋4)≤0的解集．
，则下列命题：
则
则
则
的图象关于原点对称
,
总有
1，3，2
+3
，集合B＝
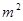
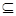A，则实数