题目内容
已知f(x)在(-1,1)上有定义,f(![]() )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(![]() )
)
⑴证明:f(x)在(-1,1)上为奇函数;?
⑵对数列x1=![]() ,xn+1=
,xn+1=![]() ,求f(xn);?
,求f(xn);?
⑶求证![]()
见解析
解析:
(Ⅰ)证明:令x=y=0,∴2f(0)=f(0),∴f(0)=0
令y=-x,则f(x)+f(-x)=f(0)=0
∴f(x)+f(-x)=0 ∴f(-x)=-f(x)
∴f(x)为奇函数 4分
(Ⅱ)解:f(x1)=f(![]() )=-1,f(xn+1)=f(
)=-1,f(xn+1)=f(![]() )=f(
)=f(![]() )=f(xn)+f(xn)=2f(xn)
)=f(xn)+f(xn)=2f(xn)
∴![]() =2即{f(xn)}是以-1为首项,2为公比的等比数列
=2即{f(xn)}是以-1为首项,2为公比的等比数列
∴f(xn)=-2n-1
(Ⅲ)解:![]()
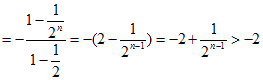
而![]()
∴![]()

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.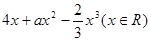 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.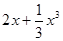 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由. 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.(12分)
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.(12分)