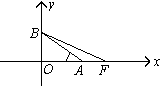题目内容
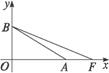
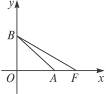
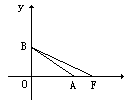
如图，OA是双曲线的实半轴，OB是虚半轴，F为焦点，且∠BAO＝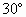
，
，则该双曲线方程是________．
答案：
解析：
解析：
|
解：根据双曲线的几何性质知|OA|＝a，|OB|＝b，|AB|＝|OF|＝c，∵∠BAO＝ |
，∴a＝
b，c＝2b，于是
|AB|·|AF|·sin
c·(c－a)＝
2b·(2b－
，由已知可得
，∴
＝3，从而
＝9，故双曲线方程为
＝1．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
，则双曲线的方程是（ ）
=1 B. 
=1
=1 D.
=1
(6-3
),求该双曲线的方程.
，
，则设双曲线方程是 
(6-3
),求该双曲线的方程. 