题目内容
已知MP，OM，AT分别为θ（
＜θ＜
）的正弦线、余弦线、正切线，则一定有（ ）
| π |
| 4 |
| π |
| 2 |
| A、MP＜OM＜AT |
| B、OM＜MP＜AT |
| C、AT＜0M＜MP |
| D、OM＜AT＜MP |
分析：作出角θ的三角函数线图象，由图象进行判断 即可得到OM＜MP＜AT
解答：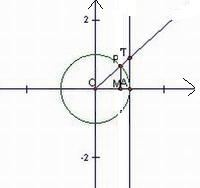
解：由MP，OM，AT分别为θ（
＜θ＜
）的正弦线、余弦线、正切线，如图
由于
＜θ＜
，所以OM＜MP
又由图可以看出MP＜AT
故可得OM＜MP＜AT
故选B．
解：由MP，OM，AT分别为θ（| π |
| 4 |
| π |
| 2 |
由于
| π |
| 4 |
| π |
| 2 |
又由图可以看出MP＜AT
故可得OM＜MP＜AT
故选B．
点评：本题的考点是三角函数线，考查用作图的方法比较三角函数的大小，本题是直接比较三角函数线的大小，在大多数此种类型的题中都是用三角函数线比较三个函数值的大小．
练习册系列答案
天天练口算系列答案
相关题目
＜θ＜
）的正弦线、余弦线、正切线，则一定有（ ）
＜θ＜
）的正弦线、余弦线、正切线，则一定有（ ）