题目内容
【题目】已知函数![]() (e为自然对数的底数).
(e为自然对数的底数).
(I)若![]() 的单调性;
的单调性;
(II)若![]() ,函数
,函数![]() 内存在零点,求实数a的取值范围.
内存在零点,求实数a的取值范围.
【答案】(Ⅰ)答案见解析;(Ⅱ)![]() .
.
【解析】
(I)定义域为![]() ,且
,且![]() ,利用导函数讨论可得:当
,利用导函数讨论可得:当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
(Ⅱ)由函数的解析式可得![]() ,令
,令![]() ,分类讨论
,分类讨论![]() ,
,![]() 和
和![]() 三种情况可得实数a的取值范围是
三种情况可得实数a的取值范围是![]() .
.
(I)定义域为![]()
![]()
故![]() 则
则![]()
(1)若![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
(2)若![]() ,令
,令![]() .
.
①当![]() 时,则
时,则![]() ,因此在
,因此在![]() 上恒有
上恒有![]() ,即
,即![]() 在
在![]() 上单调递减;
上单调递减;
②当![]() 时,
时,![]() ,因而在
,因而在![]() 上有
上有![]() ,在
,在![]() 上有
上有![]() ;因此
;因此![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
综上,(1)当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
(2)当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增.
单调递增.
(Ⅱ)设![]() ,
,
![]() ,设
,设![]() ,
,
则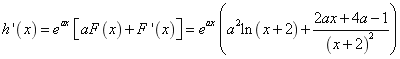 .
.
(1)若![]() ,
,![]()
![]()
![]() 在
在![]() 单调递减,
单调递减,![]()
故此时函数![]() 无零点,
无零点,![]() 不合题意.
不合题意.
(2)若![]() ,
,
①当![]() 时,
时,![]() ,由(1)知
,由(1)知![]() 对任意
对任意![]() 恒成立
恒成立![]() ,
,
故![]() ,对任意
,对任意![]() 恒成立,
恒成立,
②当![]() 时,
时,
![]()
![]() ,
,
因此当![]() 时
时![]() 必有零点,记第一个零点为
必有零点,记第一个零点为![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递增,
单调递增,![]() .
.
由①②可知,当![]() 时,
时,![]() 必存在零点.
必存在零点.
(2)当![]() ,考察函数
,考察函数![]() ,
,
由于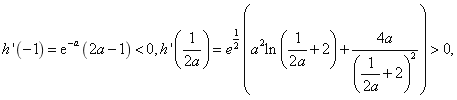
![]() 在
在![]() 上必存在零点.设
上必存在零点.设![]() 在
在![]() 的第一个零点为
的第一个零点为![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为减函数,
上为减函数,
又![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上单调递减,故当
上单调递减,故当![]() 时恒有
时恒有![]() .即
.即![]() ,
,
令![]() ,则
,则![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.![]() 即
即![]() 注意到
注意到![]() ,
,
因此![]() ,
,
令![]() 时,则有
时,则有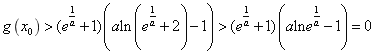 ,
,
由零点存在定理可知函数![]() 在
在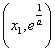 上有零点,符合题意.
上有零点,符合题意.
综上可知,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
【题目】某中学有教职工130人,对他们进行年龄状况和受教育程度的调查,其结果如下:
本科 | 研究生 | 合计 | |
35岁以下 | 50 | 35 | 85 |
35-50岁 | 20 | 13 | 33 |
50岁以上 | 10 | 2 | 12 |
从这130名教职工中随机地抽取一人,求下列事件的概率;
(1)具有本科学历;
(2)35岁及以上;
(3)35岁以下且具有研究生学历.
