题目内容
已知函数 ,数列
,数列 满足
满足 ,且
,且 .
.
(1)试探究数列 是否是等比数列?
是否是等比数列?
(2)试证明 ;
;
(3)设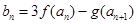 ,试探究数列
,试探究数列 是否存在最大项和最小项?若存在求出
是否存在最大项和最小项?若存在求出
最大项和最小项,若不存在,说明理由.
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
题目内容
已知函数 ,数列
,数列 满足
满足 ,且
,且 .
.
(1)试探究数列 是否是等比数列?
是否是等比数列?
(2)试证明 ;
;
(3)设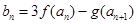 ,试探究数列
,试探究数列 是否存在最大项和最小项?若存在求出
是否存在最大项和最小项?若存在求出
最大项和最小项,若不存在,说明理由.
 全优点练单元计划系列答案
全优点练单元计划系列答案