题目内容
若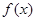 的定义域为
的定义域为 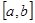 ,值域为
,值域为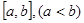 ,则称函数
,则称函数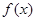 是
是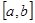 上的“四维方军”函数.
上的“四维方军”函数.
(1)设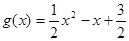 是
是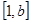 上的“四维方军”函数,求常数
上的“四维方军”函数,求常数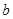 的值;
的值;
(2)问是否存在常数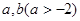 使函数
使函数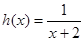 是区间
是区间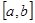 上的“四维方军”函数?若存在,求出
上的“四维方军”函数?若存在,求出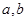 的值,否则,请说明理由.
的值,否则,请说明理由.
【答案】
(1)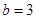 ;(2)不存在
;(2)不存在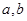 使得
使得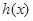 是“四维方军”函数.
是“四维方军”函数.
【解析】
试题分析:(1)由“四维方军”函数定义及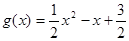 在
在 上的单调性得
上的单调性得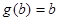 ,即可求出常数
,即可求出常数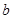 的值;(2)假设存在
的值;(2)假设存在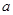 与
与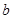 使
使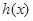 是“四维方军”函数,根据
是“四维方军”函数,根据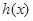 的单调性列出方程组
的单调性列出方程组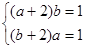 解决问题.
解决问题.
试题解析:(1)由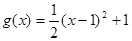 .∵
.∵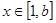 ,
,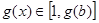 . 3分
. 3分
∴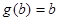 ,∴
,∴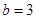 .
5分
.
5分
(2)假设存在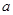 与
与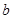 使
使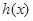 是“四维方军”函数.∵
是“四维方军”函数.∵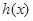 在
在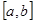 上单调递减,∴
上单调递减,∴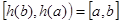 ,∴
,∴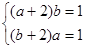 8分
8分
∴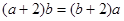 ,
10分
,
10分
∴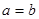 ,这与已知
,这与已知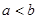 矛盾,
12分
矛盾,
12分
∴不存在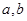 使得
使得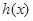 是“四维方军”函数.
13分
是“四维方军”函数.
13分
考点:函数的定义域、值域及单调性.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
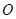 为坐标原点,
为坐标原点,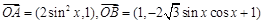 ,
,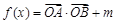 .
.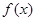 的定义域为
的定义域为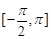 ,求
,求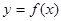 的单调递增区间;
的单调递增区间;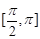 ,值域为
,值域为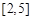 ,求
,求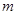 的值.
的值.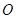 为坐标原点,
为坐标原点,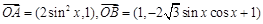 ,
,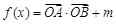 .
.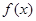 的定义域为
的定义域为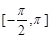 ,求
,求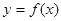 的单调递增区间;
的单调递增区间;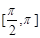 ,值域为
,值域为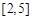 ,求
,求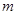 的值.
的值.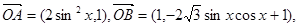
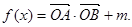
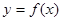 的单调递增区间;
的单调递增区间;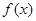 的定义域为
的定义域为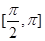 ,值域为[2,5],求m的值。
,值域为[2,5],求m的值。 为坐标原点,
为坐标原点, ,
, 。
。 的单调递增区间;
的单调递增区间; 的定义域为
的定义域为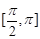 ,值域为
,值域为 ,求
,求 的值。
的值。